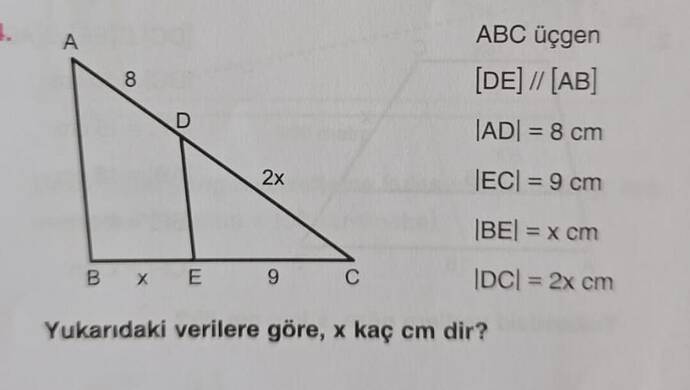
Yukarıdaki verilere göre, x kaç cm’dir?
Cevap:
Bu problemde, verilen bilgileri kullanarak \overline{BE} uzunluğunu (yani x) bulmamız gerekmektedir. Soruda, Thales Teoremi veya benzerlik teoremleri kullanılarak çözüm elde edilebilir. Thales Teoremi, paralel doğrular arasında kalan üçgenlerin benzerliği ilkesine dayanır.
Çözüm:
Bilgiye göre \overline{DE} \parallel \overline{AB}. Bu, \triangle ABC ve \triangle DEC üçgenlerini benzer yapar.
Benzerlik oranlarından dolayı şu ilişkileri yazabiliriz:
\frac{\overline{AD}}{\overline{DB}} = \frac{\overline{EC}}{\overline{BC}}
Bu eşitliği verilen uzunluklarla dolduralım:
- \overline{AD} = 8 cm
- \overline{EC} = 9 cm
- \overline{DB} = \overline{AB} - \overline{AD} = (x + 8) - 8 = x cm
- \overline{BC} = \overline{BE} + \overline{EC} = x + 9 cm
Yerine yazdığımızda:
\frac{8}{x} = \frac{9}{x + 9}
Bu oranları eşitleyip içler dışlar çarpımı yaparak denklemimizi çözelim:
8(x + 9) = 9x
Parantezleri açalım:
8x + 72 = 9x
Her iki taraftan 8x çıkaralım:
72 = x
Sonuç olarak, x 72 cm olarak bulunur.
Çözüm Özeti Tablosu
| Bilgiler | Değerler |
|---|---|
| \overline{AD} | 8 cm |
| \overline{EC} | 9 cm |
| \overline{DB} | x cm |
| \overline{BC} | x + 9 cm |
| Sonuç: x | 72 cm |
Bu şekilde Thales Teoremi ve benzerlikten faydalanarak verilen problemi çözebiliriz. Eğer başka bir sorunuz veya ek bir açıklama isterseniz, lütfen belirtin.
@username