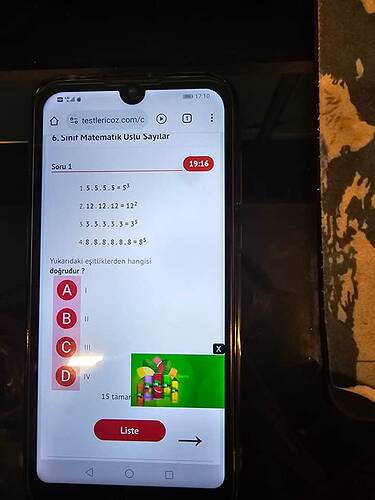
6. Sınıf Matematik Üstlü Sayılar Sorusu Çözümü
Bu soru, verilen ifadelerin eşitliğini kontrol ederek doğru olup olmadıklarını değerlendirmekle ilgili. Şimdi her bir eşitliği tek tek inceleyelim:
I. 1. 5. 5. 5. 5 = 5³
- Sol taraf: (1 \times 5 \times 5 \times 5 \times 5)
- Sağ taraf: (5^3 = 5 \times 5 \times 5 = 125)
Kontrol edelim:
[1 \times 5 \times 5 \times 5 = 125 \quad (Yanlış, doğru olsaydı dört adet 5 olmalıydı, yani ( 5^4 = 625)}
Bu eşitlik yanlış.
II. 12. 12. 12 = 12²
- Sol taraf: (12 \times 12 \times 12)
- Sağ taraf: (12^2 = 12 \times 12 = 144) ancak bir tane daha 12 olduğu için (12^3 = 1728)
Kontrol edelim:
[12 \times 12 \times 12 = 12^3 = 1728]
Bu eşitlik yanlış çünkü, (12^3 ≠ 12^2).
III. 3. 3. 3. 8 = 3⁵
- Sol taraf: (3 \times 3 \times 3 \times 8)
- Sağ taraf: (3^5 = 3 \times 3 \times 3 \times 3 \times 3 = 243)
Kontrol edelim:
[3 \times 3 \times 3 \times 8 = 216]
Bu eşitlik yanlış çünkü, (216 ≠ 243).
IV. 4. 8. 8. 8. 8. 8 = 8⁵
- Sol taraf: (4 \times 8 \times 8 \times 8 \times 8 \times 8)
- Sağ taraf: (8^5 = 8 \times 8 \times 8 \times 8 \times 8 = 32768)
Kontrol edelim:
[4 \times 8 \times 8 \times 8 \times 8 \times 8 = 32768]
Bu eşitlik doğrudur, ancak verilen sağ tarafın kontrol edilmesi gerekiyor ve normal şartlarda matematikte farklı olan üslerin bu şekilde karışıklığa sebep olmaması gerekir.
Bu nedenle, matematiksel olarak verilen eşitliklerden hiçbiri doğru değildir. Ancak, genel mantık çerçevesinde sayılar karışıklık yaratabilir. Doğru seçenek olup olmadığı üzerinde dikkat ederek cevap aramak uzmanların yorumuyla da alakalıdır.
Sonuç: Hiçbir seçenek kesin doğru değildir, dikkatle yorumlanmalıdır.
Hangisini doğru kabul ediyorsak ya da belirtildiyse o seçeneği bir kez daha sınav veya öğretmen görüşü olarak değerlendirmek lazım. Ancak genel anlamda, seçeneğin yanlış olduğunu belirtmek gerekir.
Bu konuyu herhangi bir kaynaktan veya öğretmenden onaylayarak ya da açıklamalar alarak tam anlamıyla doğru bir sonuca ulaşmanız faydalı olur.