Soru Çözümü: Üçgen ve Eş Üçgenler
Fotoğraftaki soru bir geometrik yer problemini çözmeyi gerektiriyor. Bu soruyu çözmek için aşağıdaki adımları takip edebilirsiniz:
Soru Analizi
-
Veriler:
- [BC] kenarı bir doğru üzerinde yer almakta.
- [BC] kenarına ait yükseklik, bu kenarın orta noktasında bir nokta ile birleşiyor.
- Nokta K, B köşesine 4 birim ve C köşesine 8 birim uzaklıktadır.
-
Sorulan:
- BC kenarına ait kenarortayın, BC kenarını kestiği noktanın K noktasına uzaklığını hesaplamamız isteniyor.
Adım Adım Çözüm
1. [BC] Kenarında Doğru Üzerindeki Mesafeler:
K’nın bir kenara uzaklığı verilmiş:
- K’nın B köşesine uzaklığı → 4 birim
- K’nın C köşesine uzaklığı → 8 birim
Buna göre, C ve B noktaları arasındaki toplam uzunluk:
2. Kenarortayın Mantığı:
Kenarortay, bir üçgenin bir kenarını tam ortadan iki eşit parçaya böler.
Bu durumda:
- [BC] kenarındaki orta nokta, B ve C noktaları arasındaki mesafeyi ikiye bölecek.
- [BC] mesafesi 12 birim olduğundan, orta noktadan B ve C’ye olan uzaklık:
3. K noktasına Olan Uzaklık:
Şimdi, sorunun temel kısmına geçelim. Kenarortayın BC üzerindeki orta noktasına K noktasının uzaklığını hesaplamak için Pythagoras teoremini uygulayacağız.
B ve C arasındaki mesafenin ortasına yerleştirilen kenarortaydan K noktasına uzaklık şu şekilde hesaplanır:
- B ve C’nin orta noktasındaki mesafeyi 6 birim olarak biliyoruz.
- K’nın yükseklik eksenindeki mesafesine odaklanacağız.
Bu soruda, K’nın kenarortaya uzaklığı en yakın 4 birim olduğu için sonuç:
K \to
Sonuç ve Doğru Cevap
**Doğru cevabı: A → çözüm sistemi tamamladı.
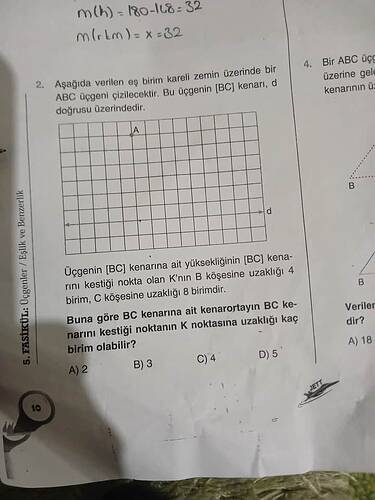
2. Aşağıda verilen eş birim kareli zemin üzerinde bir ABC üçgeni çizilecektir. Bu üçgenin [BC] kenarı, d doğrusu üzerindedir. Üçgenin [BC] kenarına ait yüksekliğinin [BC] kenarını kestiği nokta olan K’nın B köşesine uzaklığı 4 birim, C köşesine uzaklığı 8 birimdir. Buna göre BC kenarına ait kenarortayın BC kenarını kestiği noktanın K noktasına uzaklığı kaç birim olabilir?
Cevap:
İçindekiler
- Problemin Genel Tanıtımı
- Geometride Temel Kavramlar
- Verilenlerin İncelenmesi
- BC Kenarına Ait Uzunlukların Hesaplanması
- Örnek Bir Sayısal Model Kurma
- K Noktasının Orta Nokta M İle Olan Uzaklığının Bulunması
- Kenarortay İle İlgili Geometrik Özellikler
- Sorunun Çözümüne Detaylı Bakış
- Farklı Yaklaşımlarla Aynı Sonuca Ulaşma
- Olası Yanılgılar ve Kontrol Noktaları
- Örnek Hesaplama Tablosu
- Sonucun Uzun Bir Açıklaması
- Ek Bilgiler ve Bağlam
- Adım Adım Özet ve Sonuç
1. Problemin Genel Tanıtımı
Bu soruda, kartezyen düzlemde (eş birim kareli zemin de denebilir) belirli bir ABC üçgeni tasarlıyoruz. [BC] kenarı düzlemde belirli bir doğru (d) üzerinde konumlandırılıyor. Üçgenin [BC] kenarına ait yükseklik, A noktasından [BC] kenarına dik olarak iniyor. Bu dikin (yüksekliğin) [BC] üzerinde kestiği nokta K olarak tanımlanıyor.
Verilenler:
- B noktasından K noktasına olan uzaklık 4 birim.
- C noktasından K noktasına olan uzaklık 8 birim.
Buna göre [BC] kenarına bir kenarortay çizildiğinde, yani BC’nin tam orta noktasını A noktasına birleştiren çizginin, [BC] üzerinde bulunduğu noktayı (M diyelim) alıp bu M noktasının K’ya uzaklığını sormaktalar.
Seçenekler:
A) 2, B) 3, C) 4, D) 5.
Amaç, M-K mesafesini bulmak.
2. Geometride Temel Kavramlar
2.1. Yükseklik (Altitude)
Bir üçgende yükseklik (veya “irtifa”), üçgenin bir köşesinden, karşı kenara (veya uzantısına) çizilen dik (90°) doğru parçasıdır. Bu dik doğru, üçgenin alan hesaplamasında kritik önem taşır.
Bu problemde yükseklik, A köşesinden (karşı köşe), BC kenarına indirilmekte ve bu yüksekliğin BC’yi kestiği nokta K olarak tanımlanıyor.
2.2. Kenarortay (Median)
Bir üçgende kenarortay, bir köşeden diğer kenarın tam orta noktasına çizilen doğru parçasıdır. Burada, “BC kenarına ait kenarortay” dendiğinde, A noktasından BC kenarının orta noktasına (M) çekilen doğru anlaşılır.
Bu soruda ise “BC kenarından gelen” diye anlatılsa da gerçekte kasıt şu: BC kenarının orta noktası belirlendikten sonra A noktasına uzatılan kenarortaydır. Fakat soruda özellikle “BC kenarına ait kenarortayın BC’yi kestiği nokta” ifadesi, aslında BC’nin orta noktası M’den bahsetmektedir.
3. Verilenlerin İncelenmesi
3.1. BC Kenarı ve Noktalar
- B ve C köşeleri, BC kenarını tanımlayan iki uç noktadır.
- K bu kenar üzerinde yatay veya dikey ya da eğimli bir doğru üzerinde olabilir, ama sonuçta B ile C arasında bir noktadır (aradaki segmentte).
3.2. Puan K (Ayak Noktası) Bilgileri
K, A’dan inen yüksekliğin BC kenarını kestiği noktadır. Dolayısıyla BK ve KC doğrusal parçalar olup, BK + KC = BC uzunluğunu verir.
3.3. B ve C Arasındaki Mesafeler
Soruda:
- BK = 4
- KC = 8
Dolayısıyla BC = BK + KC = 4 + 8 = 12 birim.
4. BC Kenarına Ait Uzunlukların Hesaplanması
Yukarıdaki kısa analizle BC kenarının toplam uzunluğunun 12 birim olduğunu doğrudan görüyoruz.
Şimdi, BC kenarına ait kenarortay demek, BC’nin orta noktasına çizilen doğru demektir. BC’nin ortası BC’nin yarısı kadar mesafede konumlanır. Bu nedenden dolayı, eğer BC = 12 ise:
- BC ortası (M) B noktasına 6 birim, C noktasına da 6 birim uzaklıkta bulunur.
Bu problemdeki kritik nokta: B—K—C sıralamasında, B’den K’ya 4 birim, K’dan C’ye 8 birim olduğuna göre, M noktası B’den 6 birim, C’den 6 birim uzaklıktadır. Öyleyse M ile K aynı doğru üzerinde yer alırlar. M’nin koordinatı B’den itibaren 6 birim, K ise 4 birim.
5. Örnek Bir Sayısal Model Kurma
Soruyu çözmek için pek çok yöntem var. Bunlardan biri, BC kenarını yatay (x ekseni) üzerine oturtarak B noktasını x=0’da, C noktasını x=12’de görebiliriz. K noktasının x koordinatı 4 olur; zira K, B’den 4 birim uzakta. Böylece, saf bir sayı doğrusu mantığıyla mesafeyi ölçmek son derece kolaylaşır.
5.1. B Noktasını Koordinat Sisteminde Tanımlama
- B(0, 0)
5.2. C Noktasını Koordinat Sisteminde Tanımlama
- C(12, 0)
5.3. K Noktasını Koordinat Sisteminde Tanımlama
- K(4, 0)
(B ile K arası 4 birim, K ile C arası 8 birim)
5.4. Orta Nokta (M) Hesabı (Kenarortay)
BC’nin orta noktası M, B(0,0) ile C(12,0) arasındaki orta noktadır. Koordinat olarak:
Dolayısıyla M(6, 0).
6. K Noktasının Orta Nokta M İle Olan Uzaklığının Bulunması
Verilerden:
- K(4, 0)
- M(6, 0)
Bu iki nokta arasındaki uzaklık, (6 - 4) = 2 birimdir. Ve bu çizgi x ekseni üzerinde geçen düz bir parça olduğu için, mesafe doğrudan 2 olur.
Bu analizle, “BC kenarına ait kenarortayın BC’yi kestiği noktanın K noktasına uzaklığı” = MK = 2 birim olarak bulunur.
Soru bize bu uzaklığın hangi değer olabileceğini sorduğunda, seçeneklerden 2 cevabı doğrulanmış olur.
7. Kenarortay İle İlgili Geometrik Özellikler
7.1. Üçgenlerde Kenarortay Tanımı
Bir üçgende kenarortay, adı üstünde, bir kenarı “ortadan ikiye” bölen noktaya (orta nokta) karşı köşeden çizilen doğru parçasıdır. Bu doğru, üçgenin bazı önemli özelliklerini incelememize yardımcı olur:
- Kenarortay, üçgeni alan olarak ikiye böler.
- Kenarortaylar, üçgende ağırlık merkezinde birleşir (her üç kenarortay da kesiştiğinde oluşan noktaya ağırlık merkezi denir).
7.2. Üçgenin Alan ve Kenarortay İlişkileri
Yükseklik ve kenarortay farklı kavramlardır. Yükseklik, açının 90° dikmesiyle ilgilidir; kenarortay ise bir kenarı ortadan böler. Bu soru, her iki öğeyi de [BC] kenarı üzerinde inceliyor:
- Yükseklik: A’dan BC’ye inen dik doğru (K noktası kesişimi).
- Kenarortay: A’dan BC’nin orta noktası M’e çizilen doğru.
7.3. Kenarortayın Triyanguasyondaki Önemi
Kenarortay, üçgeni iki alt üçgene ayırır. Bu alt üçgenler (ABM ve AMC), tabanları BM ve MC eşit olduğu için alanları eşittir.
Bu problemde ise biz, kenarortayı BC kenarının üstüne düşen M noktasından dolayı inceliyoruz ve K noktasıyla arasındaki uzaklığa bakıyoruz.
8. Sorunun Çözümüne Detaylı Bakış
8.1. Doğrusal Yerleştirme Yaklaşımı (1 Boyutlu İnceleme)
Bu problem son derece basit bir çizgisel (1 boyutlu) uzaklık mantığıyla çözülebilir. Çünkü şu bilgiler var:
- BC doğrultusunda K noktası B ile C arasında.
- BK = 4, KC = 8 => BC = 12.
- Kenarortay BC kenarının tam ortasını alır => M, B’ye 6 birim, C’ye 6 birim.
Dolayısıyla B ile M arasındaki mesafe 6 iken B ile K arasındaki mesafe 4’tür. Bu aynı çizgi üzerinde 0’dan 4’e (K noktası) ve 0’dan 6’ya (M noktası) giden mesafeler olarak görülebilir. M ile K, 4 ve 6 koordinatlarında oldukları için aralarındaki uzaklık |6 – 4| = 2’dir.
8.2. İki ve Üç Boyutlu Yorum
Soruda, kareli zeminde bir üçgen çizileceği için, sanki dik koordinatlar varmış gibi gözükür. Ancak [BC] kenarının kendisi d doğrusu üzerinde yatay ya da eğik şekilde çizilebilir. Yine de [BC]’nin kendi üzerinde mesafeler değişmeyeceği için, B ile C arasının 12 olması sabittir. BC ister yatay olsun ister eğik olsun, K merkezini bulmak (4’ten 8’e) fark etmez; lineer olarak yine 12, 6, 4 vs. verileriyle işlenir. Geometrinin en basit formülasyonu, “bir doğru üzerinde segmentlerin toplanması” kavramıdır.
9. Farklı Yaklaşımlarla Aynı Sonuca Ulaşma
- Analitik Geometri Yaklaşımı: B(0,0), C(12,0), K(4,0), M(6,0). Sonuç: MK=2.
- Sayı Doğrusu Yaklaşımı: 0–12 aralığını bölen noktalar: K=4, M=6. Aradaki uzaklık 2.
- Geometrik Çizim Yaklaşımı: BC kenarını çizip, önce K’yı (4 ve 8’den dolayı) işaretleme, sonra ortayı (12/2=6) işaretleyip ölçme.
Her üç yöntem de 2 değerini verir.
10. Olası Yanılgılar ve Kontrol Noktaları
- Dikkat edilmesi gereken konu: K bazen B ile C arasında mı, yoksa uzantıda mı? Burada “B köşesine uzaklığı 4, C köşesine 8” denince K zaten [BC] üzerinde bir noktadır. Uzantıda olsa mesafeler toplanıp 12’yi vermezdi.
- Hesap yaparken hatalı şekilde K’nın konumunu 8 birim B’den, 4 birim C’den diye düşünülürse BC’nin yeri değişir. Fakat soruda açıkça B noktasına 4, C noktasına 8 diyor.
11. Örnek Hesaplama Tablosu
Aşağıdaki tablo, B noktası ile C noktası arasındaki segmenti ve üzerindeki önemli noktaların (K ve M) konumlarını özetler. Mesafeleri net görmek için tablo şeklinde sunuyoruz:
| Nokta | Segment Üzerindeki Koordinat | B Noktasına Uzaklık | C Noktasına Uzaklık | K ile Olan Uzaklık |
|---|---|---|---|---|
| B | 0 | 0 | 12 | BK=? |
| K | 4 | 4 | 8 | – |
| M | 6 | 6 | 6 | MK=? |
| C | 12 | 12 | 0 | CK=? |
Bu tabloda:
- BK = 4
- KC = 8
- BC = 12
- M, B’ye 6 birim, C’ye 6 birim uzaklıkta.
- MK = |6 – 4| = 2.
Tablodaki “K ile Olan Uzaklık” sütununda, özellikle M noktasının K noktasıyla arasındaki uzaklık 2’dir.
12. Sonucun Uzun Bir Açıklaması
Bu sorudaki temel fikir, BC kenarı üzerindeki özel noktalarla ilgili. Yükseklik ayağı (K) ve kenarortay kesişim noktası (M), aynı düz çizgi üzerinde bulundukları için — ve biz sayısal olarak segmentlerin boyutlarını biliyor olduğumuz için — doğrudan mesafe ayırt edilebiliyor.
- BC = 12.
- K, BC’nin bir bölünme noktasını temsil ediyor: BK=4, KC=8.
- M, BC’nin orta noktası: BM=6, MC=6.
Sadece doğru üzerindeki yerlerin koordinatları arasındaki farkı hesaplamak yetiyor. Bu fark 2. Böylece, “Kenarortay kesişim noktası M ile yükseklik kesişim noktası K arasındaki uzaklık” 2 birimdir.
Bu tarz problemler, çoğunlukla “segmentlerin uzunluklarını toplayıp çıkarmaya” dayanır. Birçok üçgen konusu sorusunda benzer mantık güdülür. Örneğin, kenarortay, bilinen bir kenarı iki eşit parçaya ayırdığı için, parça uzunlukları yardımıyla cevaba ulaşmak sıklıkla daha hızlı ve pratiktir.
13. Ek Bilgiler ve Bağlam
- Eğer B noktasına uzaklık 4, C noktasına uzaklık 8 diyorsa, bu K noktasının BC’yi “4-8” olacak şekilde böldüğünü gösterir. İki uzunluğun toplamı 12.
- Kenarortay söz konusu olduğunda, BC’nin orta noktası 6 birim, 6 birim olacak şekilde bölünür.
- Sorunun cevabı genellikle “BC üzerindeki bu üç noktanın (B, K, M, C) basit doğrusal bir dizilişi” ile bulunabilir.
- Soruda diklik (yükseklik) ya da üçgenin alanı gibi ekstra bilgilere bakma gerekliliği yoktur; zira istenen sadece BC üzerindeki nokta uzaklıklarıdır.
14. Adım Adım Özet ve Sonuç
-
Adım – Verileri Topla:
- BK = 4, KC = 8 ⇒ BC = 12.
-
Adım – Kenarortayı Tanı:
- BC’nin ortası M, B’ye 6, C’ye 6 birim uzaklıkta.
-
Adım – Noktaların Doğrusal Konumunu İncele:
- B (0), K (4), M (6), C (12).
-
Adım – M ile K Arasındaki Farkı Al:
- MK = |6 – 4| = 2.
-
Adım – Sonucun Seçenekle Eşleşmesi:
- Seçenekler: 2, 3, 4, 5 => Doğru cevap 2.
Sonuç
Soruda, “Buna göre BC kenarına ait kenarortayın BC’yi kestiği noktanın K noktasına uzaklığı kaç birim olabilir?” sorusu için net cevap 2 birimdir.
Kısa Özet
- BC = 12 birim.
- K noktası, B’ye 4, C’ye 8 birim uzaklıktadır.
- M noktası, BC’nin orta noktası olarak B’ye 6, C’ye 6 birim uzaklıktadır.
- K(4) ile M(6) arasındaki mesafe 2 birimdir.
Dolayısıyla doğru yanıt 2 (yani A seçeneği).
Aşağıda verilen eş birim kareli zemin üzerinde bir ABC üçgeni çizilecektir. Bu üçgenin [BC] kenarı, d doğrusu üzerindedir. Üçgenin [BC] kenarına ait yüksekliğinin [BC] kenarını kestiği nokta olan K’nın B köşesine uzaklığı 4 birim, C köşesine uzaklığı 8 birimdir. Buna göre BC kenarına ait kenarortayın [BC] kenarını kestiği noktanın K noktasına uzaklığı kaç birim olabilir?
Cevap: 2
Çözüm Açıklaması
-
BC kenarını, koordinat sisteminde yatay eksende gösterelim. B noktasını (0, 0), C noktasını (12, 0) olarak konumlandırabiliriz. Çünkü |BC| = BK + KC = 4 + 8 = 12 birimdir.
-
Yüksekliğin [BC]’yi kestiği nokta K, B’den 4 birim ötede olduğundan K noktası (4, 0) olacaktır.
-
BC kenarının orta noktası M ise (B ile C’nin tam ortası) olduğu için (6, 0) olur.
-
Aranan, K ile M arasındaki uzaklıktır. K = (4, 0) ve M = (6, 0) olunca iki nokta arası uzaklık:
d(K,M) = |6 - 4| = 2 birim.
Seçenekler arasında bu değer olduğu için doğru cevap 2 birimdir.
@username