Matematik dik prizmalr

YKS TYT
1

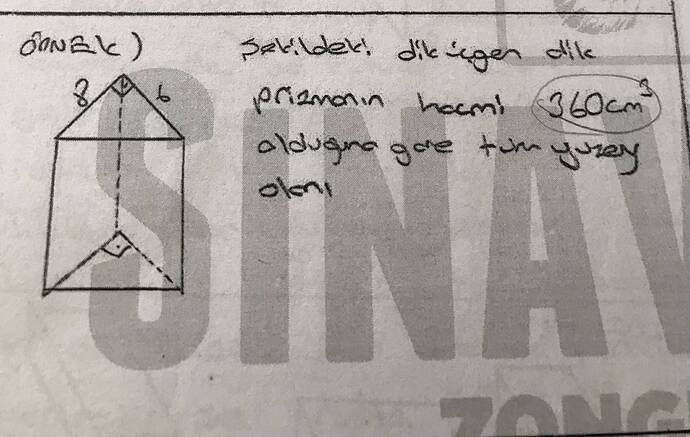
görüntü
görüntü3023×1916 544 KB

2

Şekildeki dik üçgen dik prizmanın hacmi 360 cm³ olduğuna göre tüm yüzey alanı nedir?

Cevap:

Dik üçgen dik prizmanın yüzey alanını hesaplamak için önce prizmanın temel geometrik özelliklerinden başlayalım.

Çözüm Adımları:

  1. Taban Alanının Hesaplanması:

    • Dik üçgenin kenar uzunlukları 8 cm ve 6 cm olarak verilmiştir.
    • Dik üçgenin alanı:
      A_{taban} = \frac{1}{2} \times (taban) \times (yükseklik) = \frac{1}{2} \times 8 \times 6 = 24 \, \text{cm}^2

  2. Prizmanın Hacmi ile Yüksekliği Belirleme:

    • Prizmanın hacmi formülü: Hacim = Taban \, Alanı \times Yükseklik.
    • Buna göre prizmanın yüksekliği:
      24 \times h = 360 \\ h = \frac{360}{24} = 15 \, \text{cm}

  3. Tüm Yüzey Alanının Hesaplanması:

    • Prizmanın iki üçgen tabanı ve üç dikdörtgen yan yüzü vardır.

    • İki üçgen taban alanı:

      2 \times 24 = 48 \, \text{cm}^2

    • Üç dikdörtgen yüzey:

        1. Dikdörtgen: Yükseklik \times bir kenar (15 \times 8 = 120 \, \text{cm}^2)
        1. Dikdörtgen: Yükseklik \times diğer kenar (15 \times 6 = 90 \, \text{cm}^2)
        1. Dikdörtgen: Yükseklik \times hipotenüs (Önce hipotenüsü bulalım):
        c = \sqrt{8^2 + 6^2} = \sqrt{64 + 36} = \sqrt{100} = 10 \, \text{cm}
        1. Dikdörtgen: (15 \times 10 = 150 \, \text{cm}^2)

    • Toplam yüzey alanı:

      48 + 120 + 90 + 150 = 408 \, \text{cm}^2

Bu nedenle, tüm yüzey alanı \boxed{408 \, \text{cm}^2}'dir.