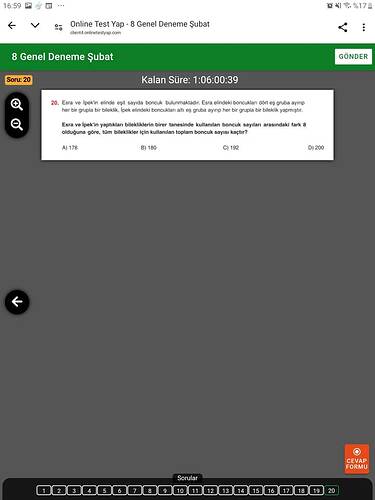
Esra ve İpek’in yaptıkları bilekliklerin birer tanesinde kullanılan boncuk sayıları arasındaki fark 8 olduğuna göre, tüm bileklikler için kullanılan toplam boncuk sayısı kaçtır?
Cevap: Bu soruyu çözmek için Esra ve İpek’in ellerinde eşit sayıda boncuk olduğunu ve bu boncuklarla belirli sayıda bileklik yaptıklarını göz önünde bulundurarak işlem yapacağız.
Adım Adım Çözüm
-
Esra’nın Durumu:
- Esra’nın elindeki boncukları dört eş gruba ayırdığını biliyoruz. Yani Esra bir bileklik için \frac{x}{4} boncuk kullanmıştır.
-
İpek’in Durumu:
- İpek, boncuklarını altı eş gruba ayırmış. Yani İpek bir bileklik için \frac{x}{6} boncuk kullanmıştır.
-
Boncuk Sayılarının Farkı:
- Esra ve İpek’in birer bileklikte kullandıkları boncuk sayısı arasında 8 fark olduğunu biliyoruz. Buradan şu denklem çıkar:
\frac{x}{4} - \frac{x}{6} = 8 -
Bu Denklemi Çözelim:
Bulunan iki tarafı eşitlemek için önce paydaları eşitleyelim. Paydaların eşiti 12’dir:
\frac{3x}{12} - \frac{2x}{12} = 8Şimdi payları çıkaralım:
\frac{x}{12} = 8Her iki tarafı 12 ile çarparak x değerini bulalım:
x = 96 -
Sonuç:
- Toplam boncuk sayısı hem Esra hem de İpek için kullanılacak boncukların toplamını bulmalıyız. İki kişi de 96 boncuğa sahiptir ve toplamda 96 + 96 = 192 boncuk kullanılmıştır.
Sonuç Tablosu
| Kişi | Bileklik Başına Boncuk | Toplam Boncuk |
|---|---|---|
| Esra | \frac{96}{4} = 24 | 96 |
| İpek | \frac{96}{6} = 16 | 96 |
| Toplam | - | 192 |
Bu yöntemle elde ettiğimiz sonuç 192 boncuktur. Bu durumda doğru cevap seçeneği C) 192 olacaktır. İyi şanslar! ![]() @SARE_TURKMEN
@SARE_TURKMEN