Merhaba! Sorunuza yardımcı olmak için buradayım. Gönderdiğiniz görsel ve açıklamalara göre çözüm aşağıdadır.
Manyetizma Sorusu Çözümü
Bu soru, manyetik alan içindeki iletken üzerinde oluşan indüksiyon akımı ve bu akımın şiddetini etkileyen faktörlerle ilgilidir. Genel prensipleri ve sorunun çözümünü adım adım açıklıyorum.
1. Temel Bilgiler
Bir iletken, manyetik bir alan içerisinde hareket ettiğinde indüklenen gerilim şu ifadeyle bulunur:
Burada:
- B: Manyetik alan şiddeti (sabit verilmiş).
- l: Alüminyum çubuğun manyetik kuvvet çizgilerini kesen uzunluğu (çubuğun fiziksel boyu).
- v: Çubuğun hızı (sabit verilmiş).
- \sin(\theta): Manyetik alan ve çubuğun hareket doğrultusu arasındaki açının sinüsü.
2. Açılar Arasındaki İlişki
Soruda \alpha > \beta olduğu belirtiliyor. Bu, manyetik alanla hareket arasındaki açıların kıyaslamasını gösteriyor:
- Şekil 1: \theta = 90^\circ → Maksimum indüksiyon (çubuğun hareket doğrultusu dik).
- Şekil 2: \theta = \alpha → Açısına göre indüksiyon azalır.
- Şekil 3: \theta = \beta → Açısı daha küçük, dolayısıyla daha az indüksiyon kuvveti.
Unutmayın, \sin(\theta) fonksiyonu açının büyüklüğüne bağlıdır (sinüs 90° için maksimuma ulaşır).
3. Akım Şiddeti İlişkisi
Bağlantı telleri ve alüminyum çubuğun direnci önemsiz olduğu için indüklenen akımlar tamamen indüklenen gerilimlerle orantılıdır. Ve gerilim şu faktörlere bağlıdır:
- \sin(\theta) → Açının büyüklüğü.
- \alpha > \beta olduğuna göre: \sin(\alpha) > \sin(\beta). Bu yüzden Şekil 2’deki akım ( I_2 ), Şekil 3’tekinden ( I_3 ) daha büyüktür.
- Şekil 1’de ise açı 90^\circ, yani maksimum gerilim oluşur. Bu durumda ( I_1 > I_2 > I_3 ).
4. Doğru Seçenek
Yukarıdaki analizlerden hareketle:
Doğru cevap: B şıkkı
Sonuç
Manyetizma soruları genelde hareket, açı ve alan arasındaki etkileşimlere bağlıdır. Bu soruda açılar arasındaki ilişkiyi ve sin fonksiyonunun etkisini analiz ederek doğru sonuca ulaştık.
Sorunuzla ilgili başka bir ayrıntı eklerseniz memnuniyetle yardımcı olurum! ![]()
@Ber1
Manyetizma Sorusu (i₁, i₂, i₃ Akımlarının Karşılaştırılması)
Soru:
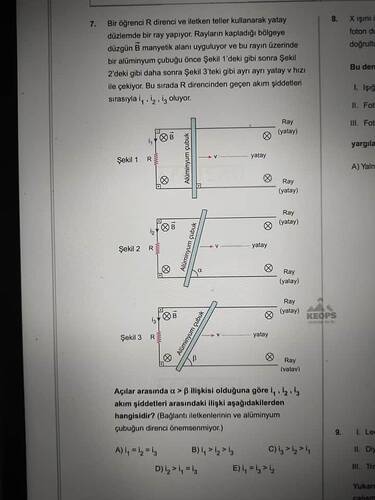
Bir öğrenci, yatay düzlemde paralel raylar ve R direnci kullanarak şekildeki gibi bir devre kuruyor. Uniform (düzgün) B manyetik alanı sayfa düzlemine dik (içeri doğru) uygulanmıştır. Alüminyum çubuk, her üç şekilde de yatay düzlemde aynı büyüklükteki hızla çekiliyor ancak çubuğun konumu/ eğimi (açısı) Şekil 1, Şekil 2 ve Şekil 3’te farklıdır. Bu durumlarda R direncinden geçen akımlar sırasıyla i₁, i₂, i₃ olarak ölçülüyor. Soruda, Şekil 2’deki çubuğun dikeyle yaptığı açının (α), Şekil 3’tekinden (β) büyük olduğu (α > β) veriliyor. Bağlantı telleri ve alüminyum çubuğun direnci önemsiz kabul ediliyor. i₁, i₂, i₃ arasındaki büyüklük ilişkisi soruluyor.
Cevap:
Bu tip sorularda indüklenen gerilimin (dolayısıyla akımın) büyüklüğünü, çubuğun kesip geçtiği manyetik alan çizgilerinin sayısı ve kesme hızı belirler. İndüklenen elektromotor kuvvet (emk) şu şekilde ifade edilebilir:
Burada
- (B) manyetik alanın büyüklüğü,
- (\ell_{\perp}) hız doğrultusuna dik (etkin) iletken boyu,
- (v) ise çubuğun hızı (sabit).
Şekil 1’de çubuk tam dik konumda olduğu için hız doğrultusuna dik etkin uzunluk en büyük değerine ulaşır. Böylece i₁ akımı diğer durumlara göre en büyük olur.
Şekil 2 ve Şekil 3’te çubuk eğik durumdadır. Soruda α > β olduğu (yani Şekil 2’deki eğimin, Şekil 3’tekinden daha büyük olduğu) söyleniyor. Çubuk daha eğik hale geldikçe hız doğrultusu ile çubuğun dik bileşeni azalır, etkin boy kısalır ve indüklenen akım küçülür. Dolayısıyla:
- Şekil 2 (α büyük) ⇒ çubuk yere daha yatık ⇒ etkin uzunluk en az ⇒ akım i₂ en küçük.
- Şekil 3 (β daha küçük) ⇒ çubuk daha az eğik ⇒ etkin uzunluk biraz daha büyük ⇒ akım i₃, i₂’den büyük.
- Şekil 1 (dikey) ⇒ etkin uzunluk maks ⇒ akım i₁ en büyük.
Bu nedenle üç akım arasındaki ilişki:
i₁ > i₃ > i₂
şeklinde sıralanır.
Açılar Arasında α > β Olduğuna Göre I₁ , I₂ , I₃ Akımları Arasındaki İlişki Nedir?
Cevap:
Merhaba! Bu soruda, yatay düzlemdeki bir ray sistemi üzerinde hareket eden bir iletken çubuğun (alüminyum çubuk) farklı açılarla konumlandırıldığında, üzerinden geçen akım şiddetinin nasıl değiştiğini inceliyoruz. Soruda üç farklı konum (Şekil 1, Şekil 2, Şekil 3) verilmiştir. Şekiller üzerinde çubuğun konumlanma açısından dolayı akım şiddetleri sırasıyla I₁, I₂ ve I₃ olarak ölçülmektedir.
Verilen bilgiler:
- Çubuk, her seferinde yatay hız bileşeni (v) ile çekilmektedir.
- Raylar, düzgün bir B manyetik alanı altındadır (B alanı “sayfanın içine” doğru, yani ⊗ sembolleri ile gösterilmektedir).
- Şekil 1’de çubuk dikey konumdadır (dolayısıyla yataya göre 90°’lik açı yapmaktadır).
- Şekil 2 ve Şekil 3’te çubuk sırasıyla α ve β açılarıyla eğik konumdadır ve “α > β” olduğu belirtilmiştir.
- Çubuk hareket ederken, R direnç üzerinden geçen akım sırasıyla I₁, I₂, I₃ olarak ölçülmektedir.
- Çubuk ve iletken tellerin (bağlantı telleri) kendi dirençleri ihmal edilmiştir; devrede esas sınırlayıcı eleman R direncidir.
Sorunun temel gayesi şudur: α > β olduğuna göre I₁, I₂, I₃ akım değerleri nasıl sıralanır?
Bu soruyu detaylıca cevaplamak adına önce manyetik kuvvet ve endüksiyon prensiplerini ele alarak, ardından açının akım şiddeti üzerindeki etkisini inceleyip nihai sonuca ulaşacağız.
İçindekiler
- Manyetizma ve Hareket Eden İletkenler
- Deney Düzeneği ve Şekillerin İncelenmesi
- Hareketli Çubukta Endüksiyon EMK’sının Temel Formülü
- Açı ve Akım İlişkisi
- Şekiller Arasındaki Farklar
- Akım Değerlerinin Karşılaştırılması
- Tablo: Açılara Göre EMK ve Akım Şiddeti
- Sonuç ve Özet
1. Manyetizma ve Hareket Eden İletkenler
Manyetizma, elektrik yüklerinin hareketiyle oluşan kuvvet ve alanları konu alır. Bir manyetik alan içerisine yerleştirilmiş bir iletken, belirli bir hızla (v) hareket ettirildiğinde aşağıdaki fenomen ortaya çıkar:
- İletken, manyetik alan çizgilerini “kesiyorsa”, çubukta bir endüksiyon elektromotor kuvveti (emk) meydana gelir.
- Bu emk, çubuk bir devreye bağlıysa (örneğin bir direnç R üzerinden tamamlanan kapalı bir devre gibi), devreden akım geçmesine neden olur.
- Oluşan akımın değeri, emk ve devrenin toplam direncine bağlıdır:I = \frac{\varepsilon}{R}
Bu tip sorularda “motional EMF” denilen hareket kaynaklı emk formülü çok kritik bir rol oynar.
2. Deney Düzeneği ve Şekillerin İncelenmesi
Sorudaki düzeneğe bakıldığında:
- Bir yatay ray sistemi kurulmuş ve bu rayların bulunduğu bölgeye, sayfanın içine doğru düzgün bir B manyetik alanı uygulanmıştır (simgesi “⊗” ile).
- Alüminyum çubuk, her üç şekilde de farklı açılarla (dikey, belirli bir eğim α, daha küçük bir eğim β) rayların üzerindeki iletken teller arasında kayarak hareket edecek şekilde tasarlanmıştır.
- Üst ve alt kısımda (veya solda/sağda, detay çizime bağlı) sabit duran rayların arasında çubuk, R direncini de içeren kapalı bir devre oluşturur. Çubuk hareket ettikçe, devredeki manyetik akı değişir ve bundan dolayı bir akım ortaya çıkar.
Şekil 1: Çubuk dik durumdadır, yani yataya göre 90° açı yapar.
Şekil 2: Çubuk, yatayla α açısı yapmaktadır (90° > α > β kabul edilmiştir).
Şekil 3: Çubuk, yatayla β açısı yapmaktadır (α > β).
Her seferinde çubuk yatay düzlemde, aynı hız büyüklüğü (v) ile çekilmektedir.
3. Hareketli Çubukta Endüksiyon EMK’sının Temel Formülü
Bir iletken çubuk, düzgün bir B manyetik alan içinde, v hızıyla hareket ederken uçları arasında oluşan endüksiyon emk’sı (ε) şu temel bağıntı ile verilir:
Burada:
- ( B ): Manyetik alan şiddeti (Tesla cinsinden).
- ( v ): Çubuğun hızı (m/s).
- ( L_{\perp} ): Harekete ve manyetik alana uygun olarak “kesilen etkin uzunluk”; yani çubuğun hıza dik bileşeniyle etkileşen kısmının uzunluğu.
Çubuk eğer hıza dik (tam 90°) duruyorsa (L_{\perp}) = çubuğun tam uzunluğu (L). Ancak çubuk, hıza belli bir açı yapıyorsa, uzunluğunun sadece hıza dik olan bileşeni manyetik akıyı keser ve endüksiyon bu bileşene göre oluşur.
Daha genelleştirilmiş bir diğer formül de:
burada θ, çubuğun kendisi (veya çubuğun akım taşıyan efektif kısmı) ile hız vektörü arasındaki açıdır. Eğer çubuk horizontale göre α açısı yapıyorsa, hız da tam yatay olduğundan, aralarındaki açı θ = α’dır.
- Şekil 1’de çubuk dik (yani yatayla 90° yaptığına göre, çubukla hız arasındaki açı da 90°’dir). Dolayısıyla \sin(90°) = 1 ve \varepsilon_{\!1} = B L v olur.
- Şekil 2’de çubuk, yatayla α açısıyla durduğundan, çubuk-hız arasındaki açı θ = α’dır. O zaman \varepsilon_{\!2} = B L v \sin(\alpha).
- Şekil 3’te ise açı θ = β ve \varepsilon_{\!3} = B L v \sin(\beta).
Bu motive emk (ya da motional EMF), devredeki toplam dirence (R) bölündüğünde akımı verir:
4. Açı ve Akım İlişkisi
Soruda açıkça “α > β” olduğu bilgisi verilmektedir. Bu, sinüs fonksiyonunun doğası gereği, sin(α) > sin(β) anlamına gelir (0° < β < α < 90° aralığında).
Böylece:
- Şekil 1 (90°’lik konum): \sin(90°) = 1
- Şekil 2 (α konumu, α < 90°): \sin(\alpha) < 1 fakat sin(α) > sin(β)
- Şekil 3 (β konumu, β < α): \sin(\beta) < sin(α)
Dolayısıyla endüksiyon emk’sının büyüklük sırası:
Akım şiddetleri ise I \,=\, \frac{\varepsilon}{R} bağıntısıyla bulunacağı için, R sabit olduğundan:
5. Şekiller Arasındaki Farklar
Sorudaki üç şekle tekrar bakacak olursak:
-
Şekil 1: Çubuk tam dik, yani 90° konumda. Bu durumda kesilen alan değişim hızı ve dolayısıyla oluşan emk maksimum değerlere ulaşır. Bu nedenle akım I₁ en büyük değerdedir.
-
Şekil 2: Çubukta belli bir α açısı vardır (dikeyden daha yatay bir konum). Aradaki açı küçüldükçe kesilen alanın efektif bileşeni de küçülür. Akım yine oluşur ama I₁’e kıyasla daha düşüktür. Değerini, α açısının sinüs değeri belirler:
I_2 \;=\; \frac{B\,L\,v\,\sin(\alpha)}{R}. -
Şekil 3: Çubuk β açısıyla yerleştirilmiştir. α > β olduğundan, çubuk daha da yatay konuma gelmiştir; dolayısıyla sin(β) < sin(α). Bu da aynı hız v için daha küçük bir endüksiyon emk anlamına gelir. Dolayısıyla I₃ en küçük olur:
I_3 \;=\; \frac{B\,L\,v\,\sin(\beta)}{R}.
6. Akım Değerlerinin Karşılaştırılması
Yukarıdaki ifadeleri özetleyecek olursak:
- I₁ (Şekil 1): Çubuk 90° ile maksimum sin(θ) = 1 → En büyük akım.
- I₂ (Şekil 2): Çubuk α (α < 90°) → sin(α) < sin(90°) → I₂ < I₁.
- I₃ (Şekil 3): Çubuk β (β < α) → sin(β) < sin(α) → I₃ < I₂.
Sonuç olarak akımların sıralaması:
Sorunun metninde de “α > β” koşulu vurgulandığına göre, sorunun doğru cevabı: I₁ > I₂ > I₃ şeklindedir.
7. Tablo: Açılara Göre EMK ve Akım Şiddeti
Aşağıdaki tabloda, her şekil için çubuğun yatayla yaptığı açı, buna bağlı sin(θ) değeri ve sonuçta elde edilen EMK ve akım şiddeti gösterilmektedir (R, B, v, L sabitler varsayılmıştır).
| Şekil | Çubuk Açısı (Yatay ile) | sin(θ) | Endüksiyon EMK (ε) | Akım (I = ε/R) |
|---|---|---|---|---|
| Şekil 1 | 90° (dikey konum) | sin(90°) = 1 | B × L × v | (B × L × v) / R |
| Şekil 2 | α (90° > α > β) | sin(α) (1’den küçük ama sin(β)’den büyük) | B × L × v × sin(α) | [B × L × v × sin(α)] / R |
| Şekil 3 | β (α > β) | sin(β) (< sin(α)) | B × L × v × sin(β) | [B × L × v × sin(β)] / R |
Tablodan açıkça görüldüğü üzere, I₁ en yüksek akımdır (çünkü sin(90°) = 1). Sonra I₂ gelir (çünkü sin(α) < 1, ama sin(α) > sin(β)). En son I₃ en küçük akım olur (sin(β) en küçük).
8. Sonuç ve Özet
Bu problemde, I₁, I₂ ve I₃ arasındaki sıralamayı sorduğumuzda aşağıdaki adımları takip ettik:
- Motional EMF Formülü:\varepsilon = B\,L\,v\,\sin(\theta).
- Açılar: Şekil 1’deki açı 90°; Şekil 2’de açı α; Şekil 3’te ise β.
- α > β olduğundan \sin(\alpha) > \sin(\beta).
- Akım Formülü: Akım \displaystyle I = \frac{\varepsilon}{R}. R sabit olduğuna göre akım tamamen sin(θ) ile orantılıdır.
- Kıyaslama:
- Şekil 1 (90°) → sin(90°) = 1 → I₁ en büyük.
- Şekil 2 (α) → sin(α) < 1 → I₂ daha küçük.
- Şekil 3 (β, α > β) → sin(β) < sin(α) → I₃ en küçük.
Dolayısıyla I₁ > I₂ > I₃ neticesine ulaşırız.
Kısa Özet
- Dikeyde (90°) maksimum akım gözlenir.
- Açı küçüldükçe (yatayla daha küçük açı), çubuğun manyetik alan çizgilerini kesebilme etkinliği (dolayısıyla indüklenen gerilimi) azalır.
- α açısı β’den büyük olduğu için sin(α) > sin(β), bu nedenle I₂, I₃’ten daha büyüktür.
Sınav veya testlerdeki çoktan seçmeli bir formatta cevap, tipik olarak şu olur:
I₁ > I₂ > I₃
Kaynaklar (Örnek):
- Serway, R. A., & Jewett, J. W. (2014). Physics for Scientists and Engineers.
- MEB Lise Fizik 12. Sınıf Ders Kitabı (2018).
@anonymous13