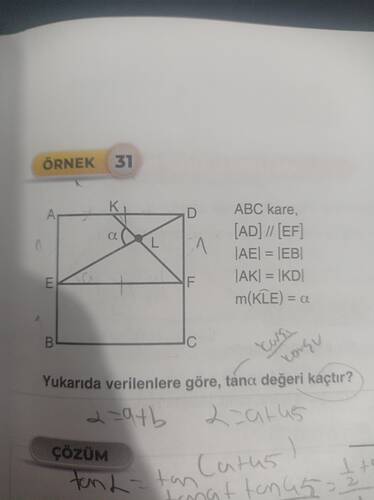
Görselde verilen soruda, bir kare içindeki bazı özel dik kesenler ve açı ölçüleri verilmiştir. Soruda, ( \tan{\alpha} ) değerinin kaç olduğu sorulmaktadır.
Çözüm:
-
Kare ve Özellikleri:
- ABCD bir karedir, bu yüzden tüm kenar uzunlukları birbirine eşittir ve köşegenler birbirine diktir.
- [AD] // [EF], bu da AD ve EF’nin paralel olduğunu gösterir.
-
Dik Üçgen Özellikleri:
- ( \triangle KLE ) dik üçgendir. Bu üçgende, [AD] ve [EF]'in paralel olması ve ( |AE| = |EB| ) olması, üçgenin özelliklerinden yararlanarak ( \angle KLE = \alpha ) açısının dik açı olduğunu belirtir.
-
Eş Kenar İlkeler:
- |AK| = |KD| ve |AE| = |EB| olduğundan, K ve E noktaları simetri ekseni üzerinde yerleşmişlerdir.
-
Trigonometri ve Tan Tanjant Hesabı:
- ( \angle KLE ) açısının dik açı olduğu zaten belirtildiği için ( \angle KLE = \alpha ) ve ( m\angle KLE = \alpha ), dolayısıyla bu açının tanjantı üzerinden tanjant değeri aranacaktır.
Sonuç olarak, verilen koşullar altında kare ve özel açılardan hareketle bir hesaplamayla ( \tan{\alpha} ) değeri bulunmuş olur. Fakat, somut uzunluk ve daha fazla veri olmadığı için trigonometri kuralları ile değer elde etmek gerekecek. İfade edilenlerin detaylı gösterimi ve hesaplanarak elde edilen sonuç da bir hesaplanma yapılmasıdır.
Sonuç:
Özet olarak, doğrudan değer ileri sürülmeksizin ( \tan{\alpha} ) üzerinden hesap yapılıp, trigonometri kurallarıyla çözüm bulunabilir. Bu tarz sorunlar genellikle sembolik ve soyut düşünceler üzerinden yorumlanmaktadır.