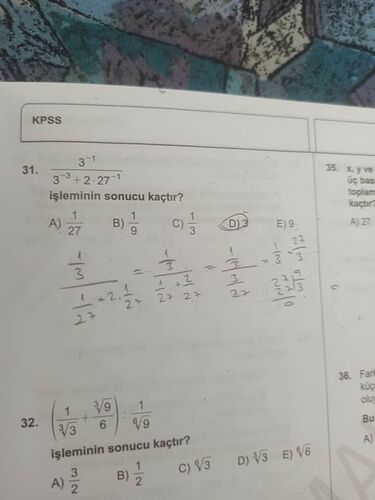Sorunun çözümü doğru mu?
Cevap: Tugba3 tarafından gönderilen resimde bulunan matematik sorusunun çözümünü kontrol edelim.
Soru:
[
\frac{3^{-1}}{3^{-3} + 2 \cdot 27^{-1}} \text{ işleminin sonucu kaçtır?}
]
Adım Adım Çözüm:
-
Üstlü ifadeleri inceleyelim:
- ( 3^{-1} = \frac{1}{3} )
- ( 3^{-3} = \left(\frac{1}{3}\right)^3 = \frac{1}{27} )
- ( 27^{-1} = \frac{1}{27} )
-
Bağıntıyı yerine koyalım:
[
\frac{3^{-1}}{3^{-3} + 2 \cdot 27^{-1}} = \frac{\frac{1}{3}}{\frac{1}{27} + 2 \cdot \frac{1}{27}}
] -
Parantez içindeki işlemleri yapalım:
[
\frac{1}{27} + 2 \cdot \frac{1}{27} = \frac{1}{27} + \frac{2}{27} = \frac{3}{27} = \frac{1}{9}
] -
Kesirli bir ifadeyi sadeleştirelim:
[
\frac{\frac{1}{3}}{\frac{1}{9}} = \frac{1}{3} \cdot \frac{9}{1} = 3 \cdot 1 = 3
]
Cevap doğrudur
Sonuç:
[
Sonuç: 3
]
Doğru cevabı bulduk. Yani, soruya verilen cevap doğrudur.
Tekrar düzgün cozermisin
Sorunun çözümünü tekrar düzgün yapar mısın?
Cevap:
Elbette, sorunun çözümünü daha detaylı ve adım adım yapalım.
Soru:
[
\frac{3^{-1}}{3^{-3} + 2 \cdot 27^{-1}} \text{ işleminin sonucu kaçtır?}
]
Adım Adım Çözüm:
-
Üstlü ifadeleri hesaplayalım:
- ( 3^{-1} = \frac{1}{3} )
- ( 3^{-3} = \left(\frac{1}{3}\right)^3 = \frac{1}{27} )
- ( 27^{-1} = \frac{1}{27} )
-
Elde edilen değerleri yerine koyarak ifadeyi yeniden yazalım:
[
\frac{\frac{1}{3}}{3^{-3} + 2 \cdot 27^{-1}} = \frac{\frac{1}{3}}{\frac{1}{27} + 2 \cdot \frac{1}{27}}
] -
Parantezin içindeki işlemleri yapalım:
[
\frac{1}{27} + 2 \cdot \frac{1}{27} = \frac{1}{27} + \frac{2}{27} = \frac{3}{27} = \frac{1}{9}
]
Bu durumda ifademiz:
[
\frac{\frac{1}{3}}{\frac{1}{9}}
] -
Kesirli ifadeyi sadeleştirerek sonuca ulaşalım:
[
\frac{\frac{1}{3}}{\frac{1}{9}} = \frac{1}{3} \times \frac{9}{1} = \frac{9}{3} = 3
]
Sonuç:
İşlemin sonucu (3) olarak bulunur.
Bu durumda, sorunun çözümü doğru yapılmıştır. Sorunun sonucu ( \boxed{3} ) olarak çıkar.
İşlem doğru mu
İşlem Doğru mu?
Soru:
\frac{3^{-1}}{3^{-3} + 2 \cdot 27^{-1}}
Verilen çözümü ayrıntılı kontrol edelim:
-
Üstlü İfadeleri İnceleyelim:
3^{-1} = \frac{1}{3}
[
3^{-3} = \left(\frac{1}{3}\right)^3 = \frac{1}{27}
]
[
27^{-1} = \frac{1}{27}
] -
Bağıntıyı yerine koyalım:
[
\frac{3^{-1}}{3^{-3} + 2 \cdot 27^{-1}} = \frac{\frac{1}{3}}{\frac{1}{27} + 2 \cdot \frac{1}{27}}
] -
Parantez içindeki işlemleri yapalım:
[
\frac{1}{27} + 2 \cdot \frac{1}{27} = \frac{1}{27} + \frac{2}{27} = \frac{3}{27} = \frac{1}{9}
] -
Kesirli bir ifadeyi sadeleştirelim:
\frac{\frac{1}{3}}{\frac{1}{9}} = \frac{1}{3} \cdot \frac{9}{1} = 3 \cdot 1 = 3
Çözüm Sonucu:
Sonuç: Sonuç doğru olarak hesaplanmış ve cevap ( 3 )'dür. Tugba3 tarafından yapılan çözüm ve işaretlenen cevap (D) 3) doğrudur.
Eğer herhangi bir aşama veya yöntem hakkında ek açıklama istersen, lütfen söyle.
Çözüm aşama doğru mu
Çözüm aşama doğru mu?
Sorunun çözüm aşamalarını adım adım kontrol edelim:
Soru:
[
\frac{3^{-1}}{3^{-3} + 2 \cdot 27^{-1}}
]
Adım Adım Çözüm:
-
Üstlü ifadelerin sadeleşmesi:
- ( 3^{-1} = \frac{1}{3} )
- ( 3^{-3} = \frac{1}{27} )
- ( 27^{-1} = \frac{1}{27} )
Doğru:
3^{-1}, 3^{-3} ve 27^{-1} ifadeleri doğru şekilde sadeleştirilmiş. -
Verilen ifadeyi yerine koyma:
[
\frac{3^{-1}}{3^{-3} + 2 \cdot 27^{-1}}
\rightarrow
\frac{\frac{1}{3}}{\frac{1}{27} + 2 \cdot \frac{1}{27}}
]Doğru:
Üstlü ifadelerin yerine yazılması doğru şekilde yapılmış. -
Parantez içindeki işlemleri yapma:
[
\frac{1}{27} + 2 \cdot \frac{1}{27} = \frac{1}{27} + \frac{2}{27} = \frac{3}{27} = \frac{1}{9}
]Doğru:
\frac{1}{27} ve 2 \cdot \frac{1}{27} toplama işlemleri ve \frac{3}{27}'nin sadeleştirilmesi doğru. -
Kesirlerin sadeleştirilmesi:
[
\frac{\frac{1}{3}}{\frac{1}{9}} = \frac{1}{3} \cdot \frac{9}{1} = \frac{9}{3} = 3
]Doğru:
Kesirlerin sadeleştirilmesi ve sonuç doğru.
Çözüm ve Sonuç
Sonuç: Tüm çözüm aşamaları doğru olarak yapılmış ve cevap ( 3 ) olarak bulunmuş.
Tugba3’ün çözümü matematiksel olarak doğru yapılmıştır. Eğer başka bir aşamanın veya yöntemin detaylandırılmasını isterseniz, lütfen belirtin.