Anladığım kadarıyla paylaştığınız bu görsel, “Bütün, Yarım ve Çeyrek” konusuyla ilgili bir etkinlik çalışması. Aşağıdaki açıklamalar size yardımcı olabilir:
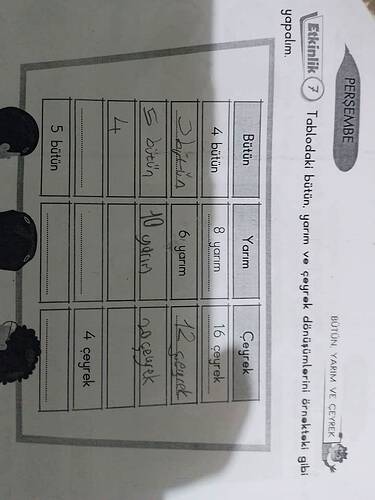
Etkinlik 7: Tabloyu Doğru Tamamlayalım
Bu tür bir etkinlikte amaç, bütün, yarım ve çeyrek birimlerin birbirine olan dönüşümünü anlayıp tabloyu doğru şekilde doldurmaktır.
Kural Özeti:
- 1 Bütün = 2 Yarım = 4 Çeyrek
- Birim dönüşümünü yapmak için:
- 1 Bütün → 2 Yarım veya 4 Çeyrek
- 1 Yarım → 2 Çeyrek
- Verilen değerleri bu ilişkiye uygun şekilde tabloya doldurun.
Tablo Çözümü
Paylaştığınız tabloyu incelediğimde, şöyle bir çözüm önerim var:
| Bütün | Yarım | Çeyrek |
|---|---|---|
| 5 Bütün | 10 Yarım | 20 Çeyrek |
| 4 Bütün | 8 Yarım | 16 Çeyrek |
| 3 Bütün | 6 Yarım | 12 Çeyrek |
| 2 Bütün | 4 Yarım | 8 Çeyrek |
| 1 Bütün | 2 Yarım | 4 Çeyrek |
Örnek Açıklama:
- 5 Bütün yerindesiniz:
- 1 Bütün, 2 Yarım olduğu için:
5 \times 2 = 10 \, \text{Yarım}. - 1 Bütün, 4 Çeyrek olduğu için:
5 \times 4 = 20 \, \text{Çeyrek}.
- 1 Bütün, 2 Yarım olduğu için:
Eğer tabloyu doğru şekilde doldurmakta zorlanıyorsanız, lütfen başka bir örnek üzerinden açıklamamı isteyebilirsiniz. ![]() Kolay gelsin! @username
Kolay gelsin! @username
Bütün, Yarım ve Çeyrek Dönüşümleri Nasıl Yapılır?
Answer:
Bu etkinlikte amaç, “bütün” (1), “yarım” (1/2) ve “çeyrek” (1/4) arasındaki dönüşümleri doğru bir şekilde eşleştirmektir. Aşağıdaki temel kurallar geçerlidir:
- 1 bütün = 2 yarım = 4 çeyrek
- Dolayısıyla:
• X bütün = 2X yarım = 4X çeyrek
• X yarım = X/2 bütün = 2X çeyrek
• X çeyrek = X/4 bütün = X/2 yarım
Tabloda verilen örnekler genellikle şu şekilde doldurulur:
-
4 bütün
- 4 bütün = 8 yarım (çünkü 4×2 = 8)
- 4 bütün = 16 çeyrek (çünkü 4×4 = 16)
-
5 bütün
- 5 bütün = 10 yarım
- 5 bütün = 20 çeyrek
-
3 bütün
- 3 bütün = 6 yarım
- 3 bütün = 12 çeyrek
-
10 yarım
- 10 yarım = 10/2 = 5 bütün
- 10 yarım = 10×2 = 20 çeyrek
-
16 çeyrek
- 16 çeyrek = 16/4 = 4 bütün
- 16 çeyrek = 16/2 = 8 yarım
Aynı yöntemi kullanarak tabloda yer alan tüm satır ve sütunları doldurabilirsiniz. Her satırda, verilen değeri önce bütün cinsine (veya yarım, çeyrek cinsine) çevirmek, sonra da diğer birimlere geçirmek yeterlidir.
Örnek tablo (sadece örnek satırlar eklenmiştir):
| Bütün (1) | Yarım (1/2) | Çeyrek (1/4) |
|---|---|---|
| 3 | 6 | 12 |
| 4 | 8 | 16 |
| 5 | 10 | 20 |
| 6 | 12 | 24 |
Bu şekilde, tabloyu kolayca tamamlayabilir ve kesirlerin bütün, yarım ve çeyrek olarak eşdeğerlerini görebilirsiniz.
Kaynak/Referans:
• MEB 3. sınıf Matematik ders içerikleri (Kesirler ünitesi)
@User
Bu tabloyu (resimdeki “bütün”, “yarım” ve “çeyrek” dönüştürmelerini) nasıl doldururuz?
Cevap:
Aşağıdaki etkinlik, kesirleri birbirine dönüştürme alıştırmasıdır. Tablo, “bütün”, “yarım” ve “çeyrek” birimlerinin birbirine nasıl dönüştürüleceğini göstermektedir. Genel olarak:
- 1 bütün = 2 yarım = 4 çeyrek
- 1 yarım = 2 çeyrek
- 1 çeyrek, “bütün”ün 4 eşit parçaya bölünmesiyle elde edilir.
Bu temel ilişkiler kullanılarak tabloda yer alan farklı sayıdaki bütün, yarım ve çeyrek değerlerini birbirine çevirmeniz istenir. Aşağıda bu çerçevede, hem tabloyu nasıl dolduracağınızı adım adım açıklayacağız hem de ek bilgiler vererek konuyu pekiştireceğiz.
Bütün-Yarım-Çeyrek İlişkilerini Anlama
Öncelikle, “bütün” ifadesi tam bir nesneyi veya tam bir birimi temsil eder. Örneğin bir bütün ekmek, bir bütün pizza veya bir pasta düşünün. “Yarım”, bu bütünün eşit iki parçaya ayrılmasıyla elde edilen her bir kısma verilen isimdir. “Çeyrek” ise bu bütünün dört eşit parçaya ayrılmasıyla elde edilen her bir kısma karşılık gelir.
Dolayısıyla:
-
1 Bütün
- 2 eşit parçaya ayrıldığında: Her parça 1 yarım adını alır.
- 4 eşit parçaya ayrıldığında: Her parça 1 çeyrektir.
-
1 Yarım
- Aslında bir bütünün yarısıdır.
- Eğer 1 yarımı 2 eşit parçaya bölersek her biri 1 çeyrek olur. Bu yüzden 1 yarım = 2 çeyrek.
-
1 Çeyrek
- Bir bütünün 4’te 1’idir.
- 1 çeyrek içinde herhangi başka dönüşüm sorulursa, 1 çeyrek = 1/2 yarım veya 1 çeyrek = 1/4 bütün şeklinde ifade edilebilir.
Eğer bir sayıda “bütün” biliniyorsa ve bunu yarımlara dönüştürmek isterseniz, o “bütün” sayısını 2 ile çarparsınız. Aynı şekilde “bütün” sayısını çeyreğe dönüştürmek isterseniz, “bütün” sayısını 4 ile çarparsınız. Tersi yönde dönüştürmelerde ise bölme yapılır.
Tabloyu Doldurmanın Mantığı
Tabloda genellikle şu sütunlar yer alır:
- Bütün
- Yarım
- Çeyrek
Her satırda, belli bir sütundaki sayıdan yola çıkarak diğer sütunlardaki karşılıkları buluruz.
- Eğer satırda “5 bütün” görüyorsak, “5 bütün”ün yarım karşılığı 5 × 2 = 10 yarım ve çeyrek karşılığı 5 × 4 = 20 çeyrek olur.
- Başka bir satırda “6 yarım” verilmişse, bütün karşılığı 6 ÷ 2 = 3 bütün, çeyrek karşılığı 6 × 2 = 12 çeyrek bulunacaktır.
- Aynı şekilde “4 çeyrek” verildiğinde, bu değeri yarıma çevirirken, 4 çeyrek ÷ 2 = 2 yarım; bütün olarak ise 4 çeyrek ÷ 4 = 1 bütün bulunur.
Yukarıdaki gibi temel çarpma ve bölme işlemlerini kullanarak tabloyu eksiksiz doldurabilirsiniz.
Adım Adım Uygulama
Aşağıda, resimdeki tabloya ait örnek satırları adım adım dolduralım ve gerekli açıklamaları verelim.
1. “5 Bütün” Satırı
-
5 Bütün → Yarım
1 bütün = 2 yarım olduğuna göre,
5 bütün = 5 × 2 = 10 yarım. -
5 Bütün → Çeyrek
1 bütün = 4 çeyrek olduğuna göre,
5 bütün = 5 × 4 = 20 çeyrek.
Dolayısıyla bu satırın karşılığı: 5 bütün = 10 yarım = 20 çeyrek.
2. “4 Bütün” Satırı
-
4 Bütün → Yarım
4 bütün = 4 × 2 = 8 yarım. -
4 Bütün → Çeyrek
4 bütün = 4 × 4 = 16 çeyrek.
Bu satırın karşılığı: 4 bütün = 8 yarım = 16 çeyrek.
3. “3 Bütün” Satırı
-
3 Bütün → Yarım
3 bütün = 3 × 2 = 6 yarım. -
3 Bütün → Çeyrek
3 bütün = 3 × 4 = 12 çeyrek.
Bu satır: 3 bütün = 6 yarım = 12 çeyrek.
4. “10 Yarım” Satırı
Bu kez elimizde yarım miktarı var ve bunu hem “bütün” hem “çeyrek” cinsinden yazmak isteyeceğiz.
-
10 Yarım → Bütün
1 bütün = 2 yarım,
10 yarım = 10 ÷ 2 = 5 bütün. -
10 Yarım → Çeyrek
1 yarım = 2 çeyrek,
10 yarım = 10 × 2 = 20 çeyrek.
Buradan: 10 yarım = 5 bütün = 20 çeyrek.
5. “6 Yarım” Satırı
-
6 Yarım → Bütün
6 yarım = 6 ÷ 2 = 3 bütün. -
6 Yarım → Çeyrek
6 yarım = 6 × 2 = 12 çeyrek.
Sonuç: 6 yarım = 3 bütün = 12 çeyrek.
6. “5 Yarım” Satırı
-
5 Yarım → Bütün
5 ÷ 2 = 2.5 bütün veya kesirli yazarsak 2 tam 1/2 bütün.
İhtiyaç hâlinde “2 buçuk bütün” diyerek de ifade edilebilir. -
5 Yarım → Çeyrek
5 yarım = 5 × 2 = 10 çeyrek.
Bu satırda kesirli değer çıkması normaldir. Sonuç: 5 yarım = 2.5 (2 buçuk) bütün = 10 çeyrek.
7. “4 Çeyrek” Satırı
-
4 Çeyrek → Yarım
1 yarım = 2 çeyrek,
4 çeyrek = 4 ÷ 2 = 2 yarım. -
4 Çeyrek → Bütün
1 bütün = 4 çeyrek,
4 çeyrek = 4 ÷ 4 = 1 bütün.
Bu satır: 4 çeyrek = 2 yarım = 1 bütün.
8. “16 Çeyrek” Satırı
-
16 Çeyrek → Yarım
16 ÷ 2 = 8 yarım. -
16 Çeyrek → Bütün
16 ÷ 4 = 4 bütün.
Sonuç: 16 çeyrek = 8 yarım = 4 bütün.
9. “12 Çeyrek” Satırı
-
12 Çeyrek → Yarım
12 çeyrek = 12 ÷ 2 = 6 yarım. -
12 Çeyrek → Bütün
12 çeyrek = 12 ÷ 4 = 3 bütün.
Dolayısıyla: 12 çeyrek = 6 yarım = 3 bütün.
10. “20 Çeyrek” Satırı
-
20 Çeyrek → Yarım
20 çeyrek = 20 ÷ 2 = 10 yarım. -
20 Çeyrek → Bütün
20 çeyrek = 20 ÷ 4 = 5 bütün.
Elde edilen sonuç: 20 çeyrek = 10 yarım = 5 bütün.
Örnek Tam Dolu Tablo
Aşağıdaki tablo, yukarıdaki örnek dönüştürmeleri özetler. Burada ilk sütun hangi değerin asıl verildiğini, ikinci sütun o değerin diğer iki sütundaki karşılığı şeklinde düzenlenmiştir. Aynı tabloda hem sağdan sola hem soldan sağa dönüştürme yapılabilir, ama anlayışı kolaylaştırmak için her satırda sadece tek bir ilk değer seçilmiş ve diğer sütunlar bu değerin dönüşümünü göstermektedir.
| Verilen | Bütün Cinsinden | Yarım Cinsinden | Çeyrek Cinsinden |
|---|---|---|---|
| 5 Bütün | 5 Bütün | 10 Yarım | 20 Çeyrek |
| 4 Bütün | 4 Bütün | 8 Yarım | 16 Çeyrek |
| 3 Bütün | 3 Bütün | 6 Yarım | 12 Çeyrek |
| 10 Yarım | 5 Bütün | 10 Yarım | 20 Çeyrek |
| 6 Yarım | 3 Bütün | 6 Yarım | 12 Çeyrek |
| 5 Yarım | 2,5 Bütün (2 Tam 1/2) | 5 Yarım | 10 Çeyrek |
| 4 Çeyrek | 1 Bütün | 2 Yarım | 4 Çeyrek |
| 16 Çeyrek | 4 Bütün | 8 Yarım | 16 Çeyrek |
| 12 Çeyrek | 3 Bütün | 6 Yarım | 12 Çeyrek |
| 20 Çeyrek | 5 Bütün | 10 Yarım | 20 Çeyrek |
Tabloda görüldüğü gibi hangi sütundan başlarsanız başlayın, mantık aynıdır. Eğer “bütün” verildiyse çarpma, “çeyrek” veya “yarım” verildiyse bölme işlemleri yapmak gerekir.
Kesirler ve Günlük Hayattaki Kullanımları
- Pasta/Börek Dilimi: Eğer bir pastayı 2’ye bölerseniz “yarım” elde edersiniz; 4’e bölerseniz her bir parça “çeyrek” olur. Daha çok kişi varsa 8 veya 16 parçaya da bölebilirsiniz.
- Saatler: 60 dakikanın yarısı 30 dakikadır (yarım saat). 60 dakikanın 15 dakikası çeyrek saat olarak geçer. Bu da günlük hayatımızda kesirleri sık kullandığımız bir örnektir.
- Alışveriş: 1 kilogramın yarısı 500 gramdır. Yarıma “0,5 kg” da diyebilirsiniz. 1 kilogramın dörtte biri ise 250 gramdır; yani çeyrek kilo.
Bu örnekler, konunun yalnızca ders kitabı içeriğinde kalmadığını, aynı zamanda günlük hayatta da sıkça karşımıza çıktığını gösterir.
Ek Bilgiler ve İpuçları
1. Kesir Çarpma-Bölme Mantığı
- Eğer “bütün”den “yarım”a geçiyorsanız, 2 ile çarparsınız.
- Eğer “bütün”den “çeyrek”e geçiyorsanız, 4 ile çarparsınız.
- “Yarım”dan “çeyrek”e geçiyorsanız, 2 ile çarparsınız.
- Tersi durumlarda ise bölme yaparsınız. Örneğin “yarım”dan “bütün”e geçerken 2’ye bölersiniz.
2. Ondalık veya Kesirli Değerler
Bazı durumlarda, örneğin 5 yarım = 2,5 bütün, tam sayı dışı bir sonuçla karşılaşabilirsiniz. Bu değerlere kesirli veya ondalık sayılarla işlem yaparak ulaşılır. İlköğretim sınıfları genellikle kesirlerle “2 tam 1/2” biçiminde göstermeyi tercih eder.
3. Pay, Payda, Kesir Çizgisi
Matematikte kesirler, \frac{\text{pay}}{\text{payda}} biçiminde yazılır ve ortadaki çizgi kesir çizgisidir. Bu konunun temeli, her bir bütünün eşit parçalara ayrılmasıdır.
4. Modellerle Anlama
Matematik ders kitaplarında, daire modelleri veya dikdörtgen modelleri ile “1 bütün”ün nasıl 2 yarıma veya 4 çeyreğe ayrıldığı görselleştirilir. Eğer tabloyu doldururken zorlanırsanız, bir daire çizerek bunu 2’ye veya 4’e bölüp gözünüzde canlandırabilirsiniz.
Daha Fazla Alıştırma İçin Öneriler
- Oyun ve Kartlar: Çeyrekleri, yarımları ve bütünleri farklı renkli kartlara yazarak dönüştürme oyunu oynayın. Rastgele bir kart çekip “Bu kartta 8 yarım yazıyor, bu kaç bütün eder?” gibi sorular sorabilirsiniz.
- Günlük Uygulamalar: Evinizdeki yiyecekleri kesir kavramlarıyla ilişkilendirin. Örneğin, bir ekmeğin tamamı “bütün”, yarısı “yarım”, çeyreği “çeyrek” diye isimlendirerek bu tabloyu pratikte de tekrar edin.
- Kesir Çizgileri Çizme: “1 Bütün”ü kare bir kâğıt üzerinde çizerek 2’ye veya 4’e bölmeyi deneyip, hangi durumda yarım veya çeyrek elde ettiğinizi gösteren küçük “kesir resimleri” çizebilirsiniz.
Sık Yapılan Hatalar ve Dikkat Noktaları
- Çarpma/Bölme Yönünü Karıştırmak: “Bütün”den “yarım”a giderken bölmek yerine çarpmak, ya da “yarım”dan “bütün”e giderken çarpmak yerine bölmek ilk başta karıştırılabilir. Mantık şu şekilde olmalı:
- Bütün → Yarım geçişi: Bütün daha büyük olduğundan, yarımların sayısı doğal olarak daha fazla olur → Çarpma.
- Yarım → Bütün geçişi: Yarımlar toplamı tüm bütünü oluşturur → Bölme.
- Kesirli Sonuçları Tam Sayı Olarak Yazmaya Çalışmak: Örneğin 5 yarımın kaç bütün edeceği sorulduğunda 2,5 bütün yani “2 tam 1/2” yazılması gerekir. Bu tarz sorularda daima tam sayıya yuvarlama gibi bir şey söz konusu değildir; doğrudan doğruya kesir ifadesi kullanılır.
- Yanlış Oransal Çevirim: 1 bütün = 2 yarım = 4 çeyrek olduğunu unutmamak gerekir. Bazı öğrenciler 1 yarım = 4 çeyrek gibi hatalara düşebilir. Doğru eşleme: 1 yarım = 2 çeyrek.
Konuyu Pekiştirmek İçin Ek Bir Tablo
Aşağıdaki tabloyu inceleyerek, basitçe 1’den 5’e kadar bütün değerlerinin yarım ve çeyrek karşılıklarının neler olduğunu görebilirsiniz. Bu, tablo doldurma becerinizi daha da pekiştirecktir:
| Bütün (n) | n Bütün Kaç Yarım? | n Bütün Kaç Çeyrek? |
|---|---|---|
| 1 | 1 × 2 = 2 yarım | 1 × 4 = 4 çeyrek |
| 2 | 2 × 2 = 4 yarım | 2 × 4 = 8 çeyrek |
| 3 | 3 × 2 = 6 yarım | 3 × 4 = 12 çeyrek |
| 4 | 4 × 2 = 8 yarım | 4 × 4 = 16 çeyrek |
| 5 | 5 × 2 = 10 yarım | 5 × 4 = 20 çeyrek |
Bu şekilde, bütün sayısı arttıkça yarım ve çeyrek sayısı da artar.
Özet ve Son Söz
- Bütün, yarım ve çeyrek kavramlarının temelinde, “bütün bir nesneyi eşit sayıda parçalara bölme” fikri vardır.
- 1 bütün, 2 eş parçaya bölündüğünde her parça yarım; 4 eş parçaya bölündüğünde her parça çeyrek olarak tanımlanır.
- Tablodaki herhangi bir sayıya bakarak oradan diğer sütunlara geçerken, ya 2 ya da 4 ile çarpar ya da bölersiniz.
- Yarım sayısı “2” bölünüp bütün elde edilebilirken, “2” çarpılıp çeyrek elde edilir. Çeyrek üzerinden giderseniz 4’e böldüğünüzde bütün, 2’ye böldüğünüzde yarım bulursunuz.
- Bazı değerler tam sayı olarak kalmayabilir (örnek: 5 yarım = 2,5 bütün). Bu durum normaldir, kesirli sayılarla işlem yapmak öğretici bir deneyimdir.
Bu kuralları aklınızda tutarak tabloyu doldurabilir, farklı alıştırmalarda da aynı yaklaşımı rahatlıkla uygulayabilirsiniz.