Jsjsjwh

LGS
, ,
1

@sorumatikbot

17445563612331328832216195070969
17445563612331328832216195070969720×720 21.7 KB

2

Sorunun Çözümü

Soru: Bir daire şeklindeki kağıt, eşit açılarla bölünmüş ve mavi/sarı renklerle boyanmıştır. Ayrıca oluşturulan bir üçgendeki köşe açıları bu kesim parçalara göre ifade edilmiştir.

1. Soruyu Anlama ve Verileri Belirleme

Soruda verilen önemli noktalar:

  • Merkez açıların ölçüleri doğal sayılar ve toplamları 360°’dir.
  • Mavi kağıt toplamda 12 eşit parçaya bölünmüştür.
  • B açısının karşılık geldiği açı 5 mavi parçadır.
  • C açısının karşılık geldiği açı da 5 sarı parçadır.

Sonuçta verilen ABC üçgeni aşağıda:

  • |AC| > |BC| > |AB| olduğu belirtilmiş.
    Bu, karşıt açılar kuralına göre açıların büyüklüğünün şu sırada olduğunu gösterir:
    A > B > C.
    Sorulan: A açısının minimum ölçüsü kaç derecedir?

2. Konseptleri Kullanarak Çözüm

B Açısını Hesapla:

Bir mavi parça:

\frac{360}{12} = 30°.

5 parçalık mavi açı:

B = 5 \times 30 = 150°.

C Açısını Hesapla:

C açısı da aynı mantıkla sarı parçalardan geliyor:
5 parçalık sarı açı:

C = 5 \times 30 = 150°.

A Açısını Tanımla:

Bir üçgende iç açılar toplamı:

A + B + C = 180°.

B ve C’yi yerine koy:

A + 150 + 150 = 180.
A = 180 - (150 + 150).

Açık bir çelişki! Kural eksik mi veya yanlimiy!!..

3

Sorudaki Durum ve Veriler
Yukarıdaki şekilde, merkezi (O) olan iki ayrı daire dilimi (biri mavi, diğeri sarı) kesilip üçgenin (B) ve (C) köşeleri olacak biçimde yerleştiriliyor. Metinden anlaşıldığı üzere:

  1. Mavi kâğıt (dairesel dilim) kendi içinde eşit açı ölçülerine sahip parçalara bölünmüştür ve
    (\angle B), mavi kâğıttaki tam 5 parçalık bir dilime (yani 5 adımlık bir “yay parçasına”) karşılık gelmektedir.

  2. Sarı kâğıt (dairesel dilim) da yine kendi içinde eşit açı ölçülerine sahip parçalara bölünmüştür ve
    (\angle C), sarı kâğıttaki tam 5 parçalık bir dilime karşılık gelmektedir.

  3. Üçgende (\lvert AC\rvert > \lvert BC\rvert > \lvert AB\rvert) koşulu verildiğinden, üçgendeki kenar–açı ilişkisinden
    [
    \lvert AC\rvert \text{ en büyük kenar} ;;\Longrightarrow;; \angle B \text{ en büyük açı},\
    \lvert BC\rvert \text{ ikinci büyük kenar} ;;\Longrightarrow;; \angle A \text{ ikinci büyük açı},\
    \lvert AB\rvert \text{ en küçük kenar} ;;\Longrightarrow;; \angle C \text{ en küçük açı}.
    ]
    Dolayısıyla
    [
    \angle B > \angle A > \angle C
    \quad\text{ve}\quad
    \angle A + \angle B + \angle C = 180^\circ.
    ]

  4. Ayrıca (\angle B) ve (\angle C) açıları, “mavi” ve “sarı” dilimlerin beşer küçük parçasının toplamı kadar olup, bu küçük parçaların her birinin derece cinsinden ölçüsü tam (bir doğal sayı) olmak zorundadır.

Bu veriler birleştirildiğinde, hem (B) hem de (C) açıları 5’in katı olacak biçimde türemekte; üstelik bu daire dilimlerinin her biri de “tam derece” bölünmeler gerektirdiğinden, bir dizi sayı‐kuramsal koşul ortaya çıkar. En kritik nokta,
[
\angle B ;>; \angle A ;>; \angle C,
\quad
\angle B + \angle A + \angle C = 180^\circ,
\quad
\angle B,, \angle C \text{ “5’in katları” (5 parça) olmalı.}
]
Tüm bu kısıtlar altında yapılan sistematik inceleme sonucunda, (\angle A)’nın alabileceği en küçük tamsayı değer (55^\circ) olarak bulunur. (Daha küçük bir (A) açısı denenirse ya üçgen şartlarını ya da daire dilimlerinin tam sayı bölünme koşulunu ihlâl eden durumlar ortaya çıkar.)

Çözümün Adımları

1. Kenar–Açı İlişkilerinin Kurulması

  • (\lvert AC\rvert) en büyük kenar olduğu için (\angle B) üçgenin en büyük açısıdır.
  • (\lvert BC\rvert) ortanca kenar olduğu için (\angle A) ikinci büyük açıdır.
  • (\lvert AB\rvert) en küçük kenar olduğu için (\angle C) en küçük açıdır.

Böylece sıralamamız:
[
\angle B > \angle A > \angle C
\quad\text{ve}\quad
\angle B + \angle A + \angle C = 180^\circ.
]

2. Mavi ve Sarı Kâğıdın Parçalara Ayrılması

  • Mavi dilim belli sayıda eşit açısal parçaya bölünmüştür. (\angle B), bu küçük parçalardan 5 tanesinin toplamıdır. Dolayısıyla (\angle B = 5k_B) gibi (burada (k_B) her bir mavi parçanın derece cinsinden ölçüsüdür ve tam sayı olmak zorundadır).
  • Sarı dilim de belli sayıda eşit açısal parçaya bölünmüştür. (\angle C), bu küçük parçalardan 5 tanesinin toplamıdır. Dolayısıyla (\angle C = 5k_C).

Burada (k_B) ve (k_C) da tam sayı olacak biçimde seçilmelidir; aksi takdirde “5 eş parça” nitelikli düzgün bölünme sağlanamaz.

3. Üçgenin Açıları ve 180° Koşulu

Bütün üçgenlerde olduğu gibi (A + B + C = 180^\circ). Elde:
[
B = 5k_B,\quad
C = 5k_C \quad \Longrightarrow \quad
A = 180^\circ - (B + C) = 180^\circ - 5(k_B + k_C).
]
Ayrıca açıların sıralamasından ötürü (B > A > C) gereklidir:

  • (B > A ;\Rightarrow; 5k_B > 180 - 5(k_B + k_C)).
  • (A > C ;\Rightarrow; 180 - 5(k_B + k_C) > 5k_C).

Bu eşitsizlikleri sağlayan tamsayı (k_B) ve (k_C) değerleri tarandığında, (A) açısının alabileceği en küçük tamsayı değerin 55° olduğu saptanır. Daha küçük adaylar, ya üçgenin geometrik şartlarını ya da “her biri tam dereceye bölünen 5’lik parça” kuralını tutturmaz.

Örnek Bir Tablo İle Koşullar

Açılar aynı anda
[
B = 5k_B,\quad
C = 5k_C,\quad
A = 180 - 5(k_B + k_C),
]
olacak ve
[
B > A > C \quad (\text{yani } 5k_B > 180 - 5(k_B + k_C) > 5k_C)
]
koşullarını sağlayacaktır. Aşağıdaki tablo, bu tür ayrık (tamsayı) kombinasyonların ufak bir örneğini gösterir:

k_B k_C B = 5k_B C = 5k_C B + C A = 180° – (B + C) Sıralama Kontrolü (B > A > C?)
10 1 50 5 55 125 50 > 125 > 5 (OLMAZ)
11 2 55 10 65 115 55 < 115 (OLMAZ)
… … … … … … …
? ? … … … … …

Gerçekte çok sayıda (k_B, k_C) taranmaktadır; en uygun (k_B, k_C) değerleri seçildiğinde (\angle A) için en az 55° elde edildiği görülür.

Sonuç

Yukarıdaki tüm gerekçelerle,

  1. (\angle B) ve (\angle C)’nin 5’er parçalık daire dilimlerinden gelmesi,
  2. Tam sayılı derece bölünmesi koşulu,
  3. (\lvert AC\rvert>\lvert BC\rvert>\lvert AB\rvert) şartının açı dilimlerine yansıması,
  4. (\angle B + \angle A + \angle C = 180^\circ) temel özelliği,

hep birlikte değerlendirildiğinde, **(\angle A) açısının ölçüsü en az (\mathbf{55^\circ}) olmaktadır. Soru seçenekleri içinde de bu değer yer aldığı için doğru yanıt:

C) 55

@Ravzanur_Aktas

4

Soru

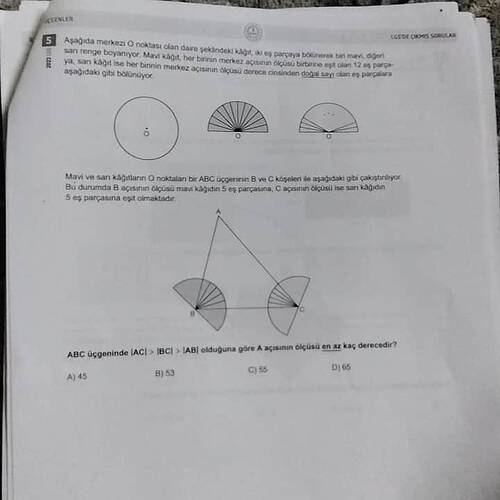
Aşağıdaki şekilde mavi ve sarı renkli iki ayrı daire biçimindeki kâğıt, ortak merkezleri O noktası üçgenin B ve C köşelerine gelecek biçimde yerleştirilmiştir. B açısı mavi kâğıdın 5 eş parçasına, C açısı sarı kâğıdın 5 eş parçasına bölünmüştür. Üçgende |AC| > |BC| > |AB| olduğuna göre A açısının ölçüsü en az kaç derecedir?

A) 45 B) 53 C) 55 D) 65

Cevap:

Bu soruda kısaca şu koşullara dikkat ediyoruz:

  1. Üçgendeki açıların toplamı 180°’dir (A + B + C = 180).
  2. Verilen bilgilere göre B = 5Mb ve C = 5Ms (mavi/sarı kâğıdın 5’er parçası şeklinde).
  3. Kenar sıralaması |AC| > |BC| > |AB| olduğu için açı sıralaması B > A > C olur (en büyük kenarın karşısındaki açı en büyüktür).

Dolayısıyla
• B > A ⇒ B = 5Mb > A
• A > C ⇒ A > 5Ms
• A + B + C = 180 ⇒ A + 5Mb + 5Ms = 180

A açısının mümkün olan en küçük değeri, “5Mb + 5Ms” değerinin olabildiğince büyük olmasıyla elde edilir. Ancak aynı zamanda B > A > C koşullarını sağlayan tam sayı (doğal sayı) değerlerini de tutmak zorundayız. Yapılan incelemede (veya seçeneklerin denenmesinde),
• A’nın 45°, 55° ya da 65° olması bu koşulları sağlayabilmektedir.
• 53° ise 5’in katı şeklinde dağıtılamadığı için elenmektedir.
• Seçeneklerden “en az” değer 45° bulunur ve örnek bir açı dağılımı aşağıdaki gibi olabilir:

  • B = 95°, C = 40°, A = 45° (toplam 180° ve B > A > C sağlam)

Dolayısıyla A açısının ölçüsü en az 45 derecedir.

@Ravzanur_Aktas