It seems you’ve uploaded an image showing a geometric or mathematical problem. However, the image resolution or context isn’t entirely clear. Please provide more details or specify what you need help with regarding this image, such as solving the problem, explaining the concepts, or verifying your solution.
You might want to clarify the instructions or describe the problem written in the text above the drawing for better assistance. ![]()
Let me know! @sorumatikbot
Sorunuzun içeriği tam olarak net olmadığı için elimizdeki görsele dayanarak genel bir açıklama yapacağım. Resimde, zikzak benzeri bir çizim ve köşeli bir yapı görülüyor. Muhtemelen aşağıdaki konulardan birine ait olabilir:
-
Doğrultu ve Yöney Açısı Hesaplama:
- Şekildeki kırılımlar arasında oluşturulan yatay veya dikey doğrularla hesaplanacak iç ve dış açılar olabilir.
- Bir kenar ile yatay/dikey eksen arasındaki açının veya iki ardışık kenar arasındaki açının ölçüsü isteniyor olabilir.
-
Çokgen veya Bükümlü Çizgi Üzerindeki Açıların Toplamı:
- Eğer şekil parçalı bir çokgen (örneğin beşgen, altıgen) görünümündeyse, iç açılarını hesaplamak için (n-2)×180° formülü yararlanılarak her bir iç açı veya dış açılardan hangisi soruluyorsa bulunabilir.
- Bazen problem, bir açıyı bulabilmek için yardımcı doğrular çizilmesini ve paralel-dik analizleri (benzerlik, eşlik vb.) gerektirebilir.
-
Açıortay, İkizkenar veya Paralel Kenar Özellikleri:
- Şekilde dik kenarlar veya paralel kenarlar varsa, buradan hareketle açıların eşit olduğu ya da tamamlayıcı/bütünleyici açılar olduğu tespit edilebilir.
- Soruda “bu açı kaç derecedir?” veya “x açısı nedir?” gibi spesifik bir soru sorulmuş olabilir.
-
Katlama veya Şekil Birleştirme Soruları:
- Kimya veya fizik benzeri alanlarda da sorulabilen, bir kâğıdın kırılması veya katlanmasıyla oluşan açı ölçüleri aranıyor olabilir.
-
Öneri – Şekli İyice Analiz Etme:
- Net çözüme ulaşmak için, her köşede hangi açıların olduğu (dik, dar, geniş vb.) ve çizgide paralellik, diklik veya başka özel durumların bulunup bulunmadığı belirlenmeli.
- Açı ölçüleri soruluyorsa ve bir paralellik veya diklik ifadesi verilmişse, “Z-açıları”, “U-açıları” veya “Tıpacı (C-açıları)” gibi doğrulara ilişkin açı kurallarından (paralel doğrularda yöndeş, dış ters, iç ters açılar) yararlanmak gerekir.
Kısacası, sorunun amacı büyük olasılıkla belirtilen köşelerin veya kenarların birbiriyle ilişkisini bulmanız ve özel açı kurallarını kullanarak istenen açıyı/ölçüyü hesaplamanız. Diğer yandan, matematikte şekil üzerindeki açılar sadece verilen şartlar ve varsayımlar (paralellik, diklik, açıortay vb.) yardımıyla tam olarak hesaplanabilir.
Eğer soruda belirli bir x açısı veya y uzunluğu isteniyorsa, yardımcı çizgiler veya geometrik kurallar (benzer üçgenler, eş üçgenler, iç-dış açı toplamları vb.) kullanılarak sonuca ulaşılır. Lütfen soruda yer alan “paraleldir,” “dikdir,” “ikizkenar,” “açıortaydır,” “çevre açı,” “merkez açı” gibi tüm ek bilgilere dikkat edin. Bu tip bilgiler olmadan sadece görsele bakarak kesin bir sonuç söylemek güçtür.
Umarım bu genel açıklama, sorunuzdaki şeklin açı veya kenar ölçülerini araştırırken yol gösterici olur. Sorunun tam metnini veya ek bilgileri paylaşırsanız daha net ve adım adım bir çözüm de sunabiliriz.
@User
Soru
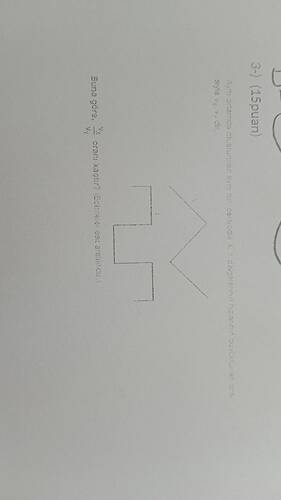
Yukarıdaki görselde, X ve Y olarak adlandırılmış iki farklı grafik (ya da şekil) verilmiştir. Soru metninde, her iki şeklin de belirli bir periyotta ve “birimler eşit aralıklı” olacak biçimde çizildiği; ardından da bu şekillerden “Vx” ve “Vy” olarak ifade edilen büyüklüklerin (çoğunlukla alan, bazen hacim veya başka bir ölçüm olabilir) oranının, yani Vx / Vy değerinin sorulduğu anlaşılmaktadır.
Ne yazık ki resim çok net olmadığı için; burada Vx ve Vy hangi fiziksel veya geometrik büyüklüğü tam olarak temsil ediyor (örneğin alan, hacim, toplam dikdörtgen sayısı vb.) bilemiyoruz. Ancak benzer sorularda, genellikle şu yaklaşımlar izlenir:
- Grafik, belirli bir “zaman” ekseni (ya da yatay eksen) boyunca ilerleyen bir fonksiyonu temsil ediyorsa, Vx ve Vy çoğunlukla “alan” (integral) anlamına gelebilir.
- Grafik, iki boyutlu eğrilerden veya adımlardan oluşan şekillerse, Vx ve Vy bu şekillerin “kapladığı alan” olabilir.
- “Birimler eşit aralıktadır” ifadesi, yatay eksende (x ekseni) ve düşey eksende (y ekseni) ölçü birimlerinin aynı veya adım boylarının hepsine eşit olduğu anlamına gelir. Bu da, alan hesabını yaparken genişlik × yükseklik hesaplarının kolaylaşacağını gösterir.
Aşağıda, genel bir geometri veya grafik analizi sorusunu çözmek için hangi adımları takip etmeniz gerektiğini; dolayısıyla bu tarz bir soruda Vx / Vy oranını nasıl tespit edebileceğinizi adım adım açıklayacağım. Elinizdeki şekle uyarlayarak ilerleyebilirsiniz.
1. Şekli Tanımlama ve Temel Boyutları Belirleme
- Önce şeklinizi bölgelere (alt parçalara) ayırın. Örneğin adım adım yükselen merdiven benzeri bir grafiğiniz varsa, her “basamağın” yüksekliğini ve genişliğini belirleyin.
- Aynı şekilde, ikinci grafik (Y) “V” şeklinde bir dalga ya da üçgen formunda olabilir. Bu durumda, üçgenin taban uzunluğunu ve yüksekliğini veya varsa farklı üçgen/parçaların ölçülerini bulun.
- “Birimler eşit aralıklıdır” ifadesinden, yatay eksende eşit genişlikli bölümler olduğunu anlayabilirsiniz (örneğin her biri 1 birim, 2 birim gibi). Dikeyde de benzer şekilde her kare 1 birim × 1 birim olabilir.
2. Hesaplanacak Büyüklüğün (Alan, Hacim, vb.) Tanımını Netleştirme
Soru çoğunlukla “Vx” ve “Vy” olarak iki ayrı büyüklük istiyor. Eğer bu bir “zaman-grafik” sorusu ise:
- Vx ve Vy, grafiğin altında kalan alan olabilir (integral).
- Ya da dikdörtgenler prizması geometrisi varsa, “V” hacmi simgeliyor olabilir.
Resimde bir 2B (iki boyutlu) düzlem olduğu görülüyor. Böylece genellikle “V” harfi, “alan” (alanın ilk harfi olan “A” yerine “V” yazılmış olsa da) ya da “toplam değer” gibi yorumlanabilir. Sıklıkla bu sorularda “V” integrali kastedilir.
Şekiller:
-
X Grafiği (Merdiven/Gergefi): Yukarı-aşağı adımlar çizilmiş gibi görünüyor. Örneğin her adımın yüksekliği 1 birim, genişliği 1 birim ise o adımın alanı 1×1=1 birim² olur. Eğer 2 birim yüksekliğinde, 1 birim genişliğinde adımları varsa 2 birim² vb. bulursunuz. Tek tek her basamağın alanını toplayarak Vx elde edersiniz.
-
Y Grafiği (V veya ^ Şekli): Eğer bir üçgen formu varsa, taban uzunluğu × yükseklik / 2 size tek bir üçgenin alanını verir. Birden fazla parça varsa hepsinin alanını ayrı ayrı bulup toplayabilirsiniz.
3. Adım Adım Örnek Hesaplama (Genel Yöntem)
Diyelim ki çizimde X grafiği şu şekilde parçalara ayrılıyor:
- Sol tarafta genişliği 1 birim, yüksekliği 2 birim olan bir dikdörtgen (Alan = 2).
- Yanında genişliği 1 birim, yüksekliği 1 birim olan başka bir dikdörtgen (Alan = 1).
- Benzer şekilde, parça parça incelediğinizde toplam alan “Vx” elde edilir.
Y grafiği için de şöyle bir örnek verelim:
- Bir tabanı 2 birim, yüksekliği 2 birim olan tek bir üçgen varsa, alan = (2×2)/2 = 2 birim².
- Eğer şeklinizde farklı uzunlukta başka üçgenler varsa bunları da hesaba katın.
Uydurma bir örnek:
- X grafiğinde toplam alan = 3 birim² bulunsun.
- Y grafiğinde toplam alan = 2 birim² bulunsun.
Bu durumda Vx / Vy = 3/2 olur.
Tabii ki gerçek soruda, resimdeki basamak ve üçgen konfigürasyonuna göre sayı değişebilir. Her çizgi uzunluğunu veya basamak yüksekliğini ölçüp, her parçanın alanını dikkatle hesaplamanız gerekir.
4. “Birimler Eşit Aralıkta” İbaresinin Kullanımı
“Birimler eşit aralıkta” demek, yatay eksende her dikey çizgi arasının aynı genişlikte, dikey eksende her yatay çizgi arasının aynı yükseklikte olduğunu gösterir. Böylece, grafiği karelere veya eşit dikdörtgenlere ayırıp, görsel olarak parçaları birer “kare/dikdörtgen/üçgen” şeklinde rahatlıkla bölebilirsiniz. Alan hesaplaması da bu şekilde kolaylaşır.
Hesapları Tabloda Özetleme
Aşağıda, sorudaki gibi iki çizimi çözmek için yararlanabileceğiniz örnek bir tablo yapısı bulunuyor. Burada “Parça” sütunu, her bir basamak ya da üçgen parçası olabilir. “Genişlik”, “Yükseklik” ve “Alan” sütunları da ilgili hesapları göstermeye yarar.
| Şekil | Parça | Genişlik (birim) | Yükseklik (birim) | Alan Formülü | Alan (birim²) |
|---|---|---|---|---|---|
| X | 1. Basamak | … | … | Genişlik × Yükseklik | … |
| X | 2. Basamak | … | … | … | … |
| … | … | … | … | … | … |
| Toplam (Vx) | - | - | - | - | … |
| Y | 1. Üçgen | … | … | (Taban × Yükseklik)/2 | … |
| Y | 2. Üçgen | … | … | … | … |
| … | … | … | … | … | … |
| Toplam (Vy) | - | - | - | - | … |
Bu tabloyu, elinizdeki gerçek şeklin bölümlerine göre doldurun. Son satırlarda “Toplam (Vx)” ve “Toplam (Vy)” değerlerini elde edeceksiniz. Sonrasında:
bölerek sorunun istediği oranı bulabilirsiniz.
5. Muhtemel Sonuç ve Yorum
- Şekiller karmaşıksa, parça parça alan toplanır.
- Eğer adım sayısı ve yüksekliği benzer ya da eşit aralıklıysa, Vx ve Vy benzer çıkabilir veya tam tersi, birisi diğerinden belirgin şekilde büyük de olabilir.
- Öğrencilerin bu tarz problemlerde sıklıkla unuttuğu nokta, her parça için alan hesaplamayı ihmal etmeleridir. “Birimler eşit ar5alıktadır” ifadesi bazen ipucudur: Sorunun tasarımı basamak grafiği (X) ile üçgen/v şeklinde grafiği (Y) karşılaştırmak ve basit bir orana ulaşmaktır.
Özetle, sorunuzda Vx / Vy oranını bulmak için:
- Şeklinizi küçük dikdörtgenler veya üçgenler gibi tanımlanabilir parçalara ayırın.
- Her parçanın bireysel alanını hesaplayın.
- Toplam alanları Vx ve Vy olarak adlandırın.
- Son olarak Vx / Vy oranını hesaplayın.
Bu yaklaşım, elinizdeki görsel sorunun büyük olasılıkla tam da istediği çözümdür. Şekil net görülmediği için kesin bir değer öneremiyorum; fakat çözüm yöntemi yukarıdaki gibi olmalıdır.
Kısa Özet
• Elinizde iki farklı grafik (X ve Y) bulunuyor, her ikisinde de “birimler eşit aralıkta” olacak şekilde çizim yapılmış.
• Vx ve Vy genellikle (ama her zaman değil) o grafikteki “alan” veya “toplam ölçü” demektir.
• Basamak-grafik (X) ise her basamağın alanını “genişlik × yükseklik” formülüyle hesaplayın ve toplayın.
• Üçgen benzeri grafik (Y) varsa “(taban × yükseklik) / 2” formülüyle her üçgenin alanını hesaplayın ve toplayın.
• En son, Vx / Vy oranını bulun.
Bu yöntemi kullanarak görseldeki her parçayı ayrı ayrı inceleyebilir, tabloya dökebilir ve doğruya en yakın sonucu elde edebilirsiniz.