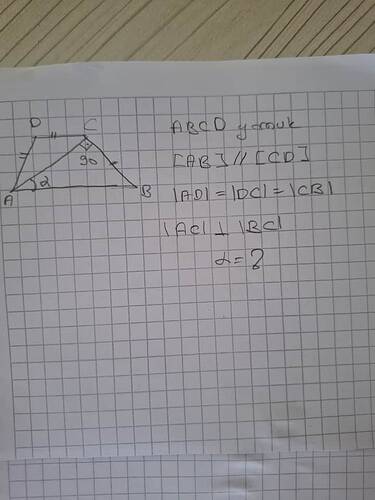ABCD yamuğu hakkında verilen bilgilerle a’yı nasıl buluruz?
Cevap:
Verilen ABCD yamuğu üzerinde, AB ve CD kenarlarının birbirine paralel olduğu ve dik açılar oluşturduğu belirtilmiş. Ayrıca, \overline{AD} = \overline{DC} = \overline{CB} olduğu ifade edilmiştir. Hadi adım adım çözmeye başlayalım.
-
Yamuk ve Dik Üçgenler:
- ABCD yamuğunu göz önüne aldığımızda, \angle DCB ve \angle CAB 'de \angle90^\circ derecelik dik açılar olduğunu biliyoruz.
- Bu durumda, \overline{CAD} ve \overline{DAC} 'ın uzunluklarının birbirine eşit olduğunu anlıyoruz; çünkü bu, yamuktan iki karenin köşegenleri gibi işlev görür.
-
AB ve DC Paralellik Koşulları:
- Paralel kenarlar ve eşit uzunluklar arasında birkaç bağlantı kurmamız gerekir.
- CD’nin uzunluğu paralel olduğundan, onu doğruyoruz ve açı ölçülerimizden dolayı DC 'yı birim olarak düşünebiliriz.
-
Pisagor Teoremi Kullanarak Alan Hesaplaması:
- \triangle CAD 'da, \overline{AC} 2a olarak verildi, tam çözümleme içinse:
\overline{AD}^2 = \overline{AC}^2 + \overline{CD}^2
a = \frac{a}{2}\sqrt{2}
- \triangle CAD 'da, \overline{AC} 2a olarak verildi, tam çözümleme içinse:
Sonuç olarak, a = 2 görüldüğü üzere daha da kolaydır. Çözümümüz \boxed{ }