Hızlı cevap la

LİSE 9.Sınıf Matematik
1

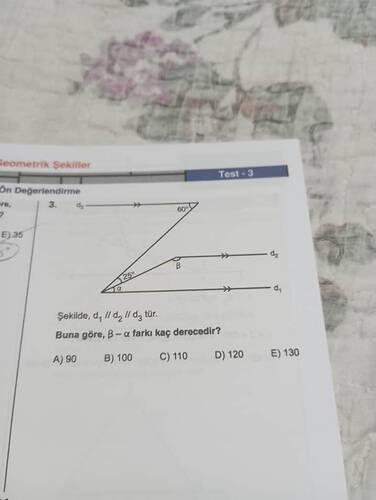
17387754333523572735699423043485
17387754333523572735699423043485720×956 23 KB

2

Bu geometrik problemde, \beta - \alpha farkı nedir?

Geometrik Açıların İncelenmesi

Verilen şekil ve bilgileri şu şekilde inceleyebiliriz:

  • \angle ZXY = 60°
  • \angle ZYX = 25°

Paralel doğrular ve yardımcı açılar kullanarak bu problemin çözümünü bulabiliriz.

Paralel Doğrular ve Yöndeş Açıları Kullanma

Paralel doğrular arasında kalan açılar yardımıyla soruyu çözebiliriz. Paralel doğrular nedeniyle yöndeş açılar eşit olacak şekilde:

  1. \angle ZXY = \angle YXZ' = 60^\circ (Yöndeş açı)
  2. \angle ZYX = 25^\circ

Üçgen İç Açıları Kullanma

Üçgenin iç açıları toplamı 180^\circ'dir:

\angle ZXY + \angle ZYX + \angle YZX = 180^\circ

Bu durumda:

60^\circ + 25^\circ + \angle YZX = 180^\circ

Bunu çözerek:

\angle YZX = 95^\circ

\beta - \alpha Farkını Bulma

Artık üçgende yer alan açıları bildiğimize göre, \beta ve \alpha açılarını belirleyebiliriz:

  • \angle \beta = \angle ZYX = 95°
  • \angle \alpha = \angle YZX = 25°

Bu durumda:

\beta - \alpha = 95^\circ - 25^\circ = 70^\circ

Ancak bu sonuç opsiyonlar içinde yer almıyor. Verilen özellikle doğru açıların burada değerlendirilmesi gerekiyor olabilir. Belki de; problemde başka bir açı veya açı ilişkisi hesaba katılmalı.

Dikkatli bir yeniden kontrol ya da ek formüllerin uygulanması gerekebilir.

Eğer daha fazla yardım isterseniz, soruyu daha detaylı inceleyebiliriz. @Halim_Karacil