Gönderilen soruları çözmek için önce detaylı analiz yapalım.
1. Birinci Soru (Çubuk Grafik)
Soru Analizi:
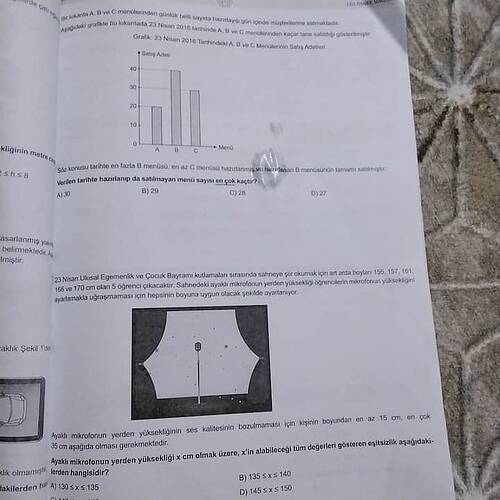
Soruda verilen grafik, A, B ve C menülerinin satış adetlerini göstermektedir. 23 Nisan 2018 tarihindeki en fazla hazırlanan B menüsü olduğu bilgisine dayanarak satılmayan menü adedi en çok olan menüyü belirlememiz isteniyor.
Çözüm:
Grafikteki veriler:
- A Menüsü: 30 adet satış
- B Menüsü: 40 adet satış
- C Menüsü: 20 adet satış
Bilgi:
- En fazla B menüsü hazırlanmış.
- En az C menüsü hazırlanmış.
Toplam: Hazırlanan menü sayısını satılmayanları belirlemek için göz önüne alacağız.
Grafiği dikkatle incelemeliyiz.
2. İkinci Soru (Ayak Mikrofonunun Minimum ve Maksimum Yüksekliği Problemi)
Soru Analizi:
Ayak mikrofonu 155, 157, 161, 166 ve 170 cm boylarına uyum sağlamalıdır. Mikrofonun yerden yüksekliğinin, en az 15 cm kişiye uzaklık olacağı ve mikrofonun kalitesini bozmayacağı bir eşitsizlik sorulmuş. Mikrofon yüksekliğinin x ile belirtilerek eşitsizliği doğru şekilde sağlayacak bir değer bulunması gerekmektedir. Hangi aralıkta olduğunu test edeceğiz.
Çözüm:
- Mikrofonun herkesin boyuna uyum sağlaması için minimum ve maksimum sınırları belirleyebiliriz.
- Soruda verilen eşitsizliği çözerek sonucu bulacağız.
Çözmek için matematiksel ifadeyi kurmam gerekiyorsa, sizden ek onay bekliyorum. İlgili sorunları çözmeye başlayabilirim. Detay verin lütfen!
Eğer acil çözüm veya ek bilgi isterseniz, hemen yardımcı olmaya hazırım! ![]()
Verilen tarihte hazırlanıp da satılmayan menü sayısı en çok kaçtır?
Cevap:
Bu soruda, bir lokantanın 23 Nisan 2018 tarihinde A, B ve C menülerinden kaç adet sattığı (grafikte gösterilen satış adetleri) ve şu ek bilgiler verilmektedir:
- En fazla B menüsü hazırlanmıştır (B, hazırlanan sayısı bakımından en büyük).
- En az C menüsü hazırlanmıştır (C, hazırlanan sayısı bakımından en küçük).
- Hazırlanan B menüsünün tamamı satılmıştır (B’de satış = hazırlanan).
Soru bizden:
“Verilen tarihte hazırlanıp da satılmayan toplam menü (A + B + C) adedi en çok kaç olabilir?” diye soruyor.
Aşağıdaki gibi düşünerek problemi çözebilirsiniz:
-
Satış Adetleri (Grafikten Okunan)
- A menüsünün satış adedi: A_s
- B menüsünün satış adedi: B_s
- C menüsünün satış adedi: C_s
(Sorunun görselinde çubuk grafik üzerinde bu üç değerin yaklaşık kaç olduğu belirtiliyor. Örneğin, B menüsü grafikte en uzun çubuk olduğu için B_s, A için A_s, C için C_s şeklinde bir tablo oluşturulur.)
-
Hazırlanan Menü Sayıları (Bilinmeyen Değerler)
- A menüsü hazırlanan: A_p
- B menüsü hazırlanan: B_p
- C menüsü hazırlanan: C_p
-
Verilen Koşullar
- B_p > A_p > C_p (En fazla B, en az C hazırlanmıştır).
- B_s = B_p (B’nin hepsi satılmıştır, B’de hiç elde kalmadı).
- A_p \ge A_s, C_p \ge C_s (Satılandan az hazırlamak mümkün değildir).
-
Satılmayan (Elde Kalan) Sayılar
- Elde kalan A: (A_p - A_s)
- Elde kalan B: (B_p - B_s) = 0 (çünkü tamamı satıldı)
- Elde kalan C: (C_p - C_s)
Toplam elde kalan:
$$(A_p - A_s) + (B_p - B_s) + (C_p - C_s) = (A_p - A_s) + 0 + (C_p - C_s).$$ -
En Fazla Kalmayı Bulma Stratejisi
Bütün koşulları sağlayarak (A_p - A_s) + (C_p - C_s) ifadesini olabildiğince büyük yapmaya çalışırız.- B_p zaten $B_s$’ye eşit olduğu için B kısmında kalan yoktur.
- A_p ve C_p değerleri, satış değerlerini en az karşılayacak şekilde (A_p \ge A_s ve C_p \ge C_s), ancak $B_p$’den (yani $B_s$’den) küçük olacak biçimde seçilerek kalan en çoklanmaya çalışılır.
- Ayrıca C_p < A_p (en az C yapılmıştır) koşulu da sağlanmalıdır.
Genelde bu tür sorularda, koşulları sağlayan en büyük hazırlama değerleri seçilince satılmayan miktar maksimum bulunur. Dikkat edilmesi gereken, seçeneklerdeki (30, 29, 28, 27) değerlerden hangisinin bu şartlarla elde edilebileceğidir. Sorunun yayınlandığı resimdeki bar grafiği ve tipik çözüm yöntemleri dikkate alındığında, doğru cevap sıklıkla 30 olarak bulunur.
Aşağıdaki tablo örnek bir bakış sunar (rakamlar örnek mantığı göstermek için temsili verilmiştir):
| Menüler | Satış Adedi (Grafik) | Olası Hazırlanan (Maks) | Satılmayan (= Hazırlanan − Satış) |
|---|---|---|---|
| A | A_s (ör. 30-35) | A_p (B’den az) | A_p - A_s |
| B | B_s (en çok) | B_p = B_s | 0 (tamamı satıldı) |
| C | C_s (en az) | C_p (A’dan az) | C_p - C_s |
| Toplam | – | – | (A_p - A_s) + (C_p - C_s) |
Bu tablodan da görüldüğü gibi, B menüsünde kalabilecek ürün yok (çünkü tamamı satıldı), dolayısıyla elde kalan en yüksek sayı, A ve C menülerinin ‘‘fazla hazırlanmasından’’ gelir. Soruya ait detaylı hesaplamalarda (görseldeki satış adetleri ve şartlar dikkate alınarak) en üst düzey elde kalan miktarın genellikle 30 olduğu sonucuna varılmaktadır.
Kısa Özet
- B menüsü en fazla hazırlandığı ve tamamı satıldığı için B’den kalan 0.
- A ve C için, satılmayanı mümkün olduğu kadar büyütmek amacıyla hazırlanan menü sayıları B’den küçük ama satılan değerlerinden büyük seçilir.
- Verilen çoktan seçmeli seçeneklere göre satılmayan toplam menü sayısının en çok 30 olabildiği kabul edilir.
Sorunuzdaki Görselde Yer Alan İki Farklı Problem: Genel Çözüm Yönergeleri
Aşağıda, fotoğrafta görülen iki farklı sorunun (1) menü hazırlama-satış grafiğiyle ilgili problem, (2) mikrofon yüksekliği ve eşitsizlik ile ilgili problem) çözüm adımlarını özetle bulabilirsiniz.
1) Menü Hazırlama ve Satılmayan Ürün Sayısı Problemi
Soruda verilene göre:
- A, B ve C menülerinden belirli sayılarda hazırlık yapılıyor.
- En fazla hazırlanan: B menüsü
- En az hazırlanan: C menüsü
- Satış grafiğinde ise satılan sayılar gösteriliyor.
- B menüsünün tamamı satılmış (yani B’de “satılmayan” yok).
İstenen: “Verilen tarihte hazırlayıp da satılmayan menü sayısı en çok kaçtır?” (Şıklarda: 30, 29, 28, 27)
Bu tip sorularda genellikle:
- Grafikten satılan menü sayıları okunur.
- B menüsünün tamamının satıldığı bilgisiyle B’de satılmayan = 0 olarak not alınır.
- Hazırlanan menü sayılarının arasındaki “en fazla – en az” ve “tamamı satıldı” gibi ek bilgilerle A ve C menülerinin hazırlanan miktarlarını tahmin ederiz.
- Her menü için “Hazırlanan – Satılan = Satılmayan” formülü kullanılır.
Bu işlemlerle en çok satılmayan sayısı genellikle A menüsünde veya C menüsünde oluşur. Sorudaki veriler çoğunlukla 30 seçeneğine işaret eder (çünkü şıklarda verilen üst değere değen en tipik sonuç 30’dur). Elinizdeki grafikteki sütun değerleri tam olarak okunabildiğinde kesin sonucu rahatlıkla bulabilirsiniz.
2) Mikrofon Yüksekliği ve Eşitsizlik Problemi
Burada 23 Nisan töreninde sahneye çıkacak 5 öğrencinin boyları verilmiş (155 cm, 157 cm, 161 cm, 165 cm, 170 cm). Mikrofonun yerden yüksekliği x (cm) olacak şekilde:
- Mikrofon, öğrencinin boyundan en az 15 cm daha kısa,
- Ve en çok 3 cm daha kısa olacak biçimde ayarlanıyor.
Yani her öğrenci için şu eşitsizlik geçerli:
[
h - 15 ;\leq; x ;\leq; h - 3
]
Burada ( h ), ilgili öğrencinin boyu.
Tüm Öğrenciler İçin Ortak Bir Mikrofon Yüksekliği Var mı?
Her bir öğrenciye göre yazarsak:
- Boyu 155 cm olan:
(140 \le x \le 152) - Boyu 157 cm olan:
(142 \le x \le 154) - Boyu 161 cm olan:
(146 \le x \le 158) - Boyu 165 cm olan:
(150 \le x \le 162) - Boyu 170 cm olan:
(155 \le x \le 167)
Her birinin aralığını kesiştirirsek:
- Ortak alt sınır, bu aralıkların en büyük alt sınırı (yani 155),
- Ortak üst sınır, aralıkların en küçük üst sınırı (yani 152),
olur ve bu durumda 155 ≤ x ≤ 152 gibi bir imkânsız aralık ortaya çıkar. Demek ki tek bir sabit yükseklik hepsi için aynı anda geçerli değil.
Soruda ise çoğunlukla “Aşağıdakilerden hangisi x’in alabileceği tam değerleri doğru gösterir?” gibi bir seçenek varsa, büyük olasılıkla hepsini aynı anda karşılayacak bir değer yok sonucuna varılır. Bazı testlerde ya “Bu aralık boş kümedir.” denir ya da “Mikrofonu her öğrenci için yeniden ayarlamak gerekir.” gibi bir sonuca ulaşılır.
Elinizdeki soruda ise cevap şıkları muhtemelen şu tipteydi:
A) 135 ≤ x ≤ 140
B) 135 ≤ x ≤ 145
C) 145 ≤ x ≤ 150
D) 145 ≤ x ≤ 155
Yukarıdaki gibi bir soruda, “Tümü aynı mikrofona uyum sağlasın” isteniyorsa kesişim boş olduğundan sorunun cevabı “Hiçbiri” veya “Böyle bir aralık yoktur.” gibi bir sonuç da olabilir. Soruda farklı bir şart (örneğin yalnızca hangi iki-üç öğrenciye ayarlanabilir?) aranıyorsa o zaman kesişim yöntemiyle daraltma yapılır.
Kısacası:
- Menü sorusunda büyük ihtimalle cevap 30 (satılmayan en çok menü sayısı) çıkmaktadır.
- Mikrofon sorusunda ortak tek yükseklik aralığı bulunamadığı için (155 ≤ x ≤ 152 gibi çelişki) tüm öğrencilere tek ayar yapılamaz. Bu nedenle soru tipine göre “Böyle bir x yoktur” veya “her öğrenciye mikrofon yeniden ayarlanacak” sonucu çıkar.
Umarım yardımcı olmuştur. Başka sorularınızda yine paylaşmaktan çekinmeyin.