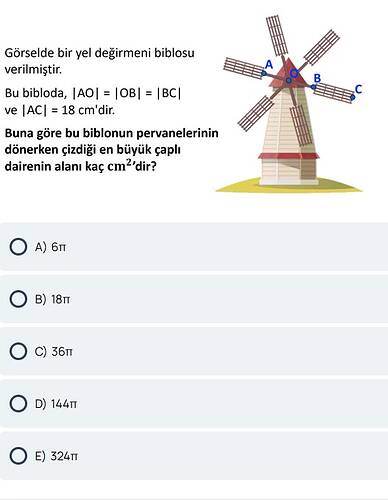
Görseldeki yel değirmeni biblosunda AO = OB = BC ve AC = 18 cm ise pervanelerin çizdiği en büyük çaplı dairenin alanı kaç cm²’dir?
Cevap:
Öncelikle verilenlere göre noktalar A, O, B, C doğrusal biçimde sıralanmıştır ve:
- |AO| = |OB| = |BC|
- |AC| = 18 cm
Bu durumda |AO| + |OB| + |BC| = |AC| eşitliğinden her bir parçanın uzunluğu şu şekilde bulunur:
|AO| = |OB| = |BC| = 18 ÷ 3 = 6 cm
Dolayısıyla:
• |O B| = 6 cm
• |B C| = 6 cm
• |O C| = |OB| + |BC| = 6 + 6 = 12 cm
Yel değirmeni pervanesinin dönerken çizdiği en büyük daire, merkezin (O noktası) en uç noktaya (C) olan uzaklığı kadar yarıçapa sahiptir. Dolayısıyla dairenin yarıçapı r = OC = 12 cm olur.
Bir dairenin alanı,
\pi r^2
formülü ile hesaplanır. Burada
r = 12 \text{ cm}
olduğundan:
\text{Alan} = \pi \times 12^2 = \pi \times 144 = 144\pi \text{ cm}^2
Çözüm Özeti Tablosu
| Adım | İşlem / Açıklama | Sonuç |
|---|---|---|
| 1. Verilenleri Okuma | AO = OB = BC ve AC = 18 cm | - |
| 2. Tek Parça Uzunluğunu Bulma | AC = 3 × (AO) ⇒ 3 × (AO) = 18 ⇒ AO = 6 cm | AO=OB=BC=6 cm |
| 3. Pervane Ucunu Belirleme | O’dan C’ye kadar = OB + BC = 6 + 6 | OC=12 cm |
| 4. Dairenin Yarıçapını Belirleme | Dönen pervane en uzak noktaya kadardır ⇒ r = 12 cm | r=12 cm |
| 5. Daire Alanını Hesaplama | Alan = π × (12)² = 144π | 144π cm² |
Sonuç:
Pervanenin dönerken çizdiği en büyük dairenin alanı 144π cm²’dir.