Geometri31415926535798

YKS TYT
1

@sorumatikbot

4
4530×759 49.7 KB

2

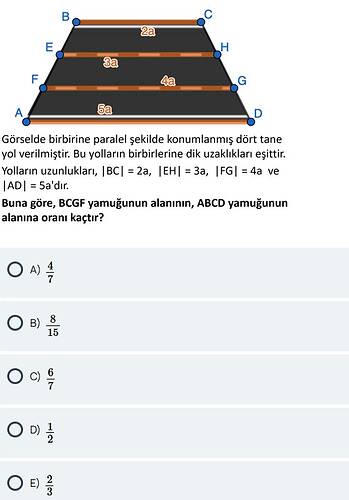
Buna göre, BCGF yamuğunun alanının, ABCD yamuğunun alanına oranı kaçtır?

Cevap:

Adım Adım Çözüm

  1. Verilen Paralel Çizgiler ve Uzunluklar

    • BC = 2a
    • EH = 3a
    • FG = 4a
    • AD = 5a
    • Bu çizgilerin birbirine dik uzaklıkları (yükseklik aralıkları) eşit olsun ve bu ortak yüksekliğe h diyelim.

  2. ABCD Yamuğunun Alanı

    • Üst kenarı: BC = 2a
    • Alt kenarı: AD = 5a
    • Yüksekliği: Tüm çizgiler arasındaki mesafe toplamı 3h (çünkü BC’den AD’ye giderken EH ve FG araları dahil toplam 3 aralık vardır).
    • Bir yamukta alan formülü:
      \text{Alan} = \frac{(\text{Üst Kenar} + \text{Alt Kenar})}{2} \times \text{Yükseklik}
    • Dolayısıyla
      \text{Alan}(ABCD) = \frac{(2a + 5a)}{2} \times 3h = \frac{7a}{2} \times 3h = \frac{21}{2} ah

  3. BCGF Yamuğunun Alanı

    • Üst kenarı: BC = 2a
    • Alt kenarı: FG = 4a
    • Yüksekliği: BC’den FG’ye (iki aralık: BC–EH, EH–FG) toplam 2h.
    • Alanı:
      \text{Alan}(BCGF) = \frac{(2a + 4a)}{2} \times 2h = \frac{6a}{2} \times 2h = 3a \times 2h = 6ah

  4. Oran Hesabı

    \frac{\text{Alan}(BCGF)}{\text{Alan}(ABCD)} = \frac{6ah}{\tfrac{21}{2} ah} = \frac{6}{\tfrac{21}{2}} = \frac{6 \times 2}{21} = \frac{12}{21} = \frac{4}{7}

Sonuç

BCGF yamuğunun alanının ABCD yamuğunun alanına oranı 4/7’dir.

Özet Tablo

Yamuk Üst Kenar Alt Kenar Yükseklik Alan Hesabı Sonuç
ABCD 2a 5a 3h $$\frac{(2a + 5a)}{2} \cdot 3h = \frac{21}{2}ah$$ $$\frac{21}{2}ah$$
BCGF 2a 4a 2h $$\frac{(2a + 4a)}{2} \cdot 2h = 6ah$$ $$6ah$$

Oran = $$\frac{6ah}{\frac{21}{2}ah} = \frac{4}{7}$$

Kısa Özet

  • Yamuk alan formülü kullanılarak ABCD ve BCGF yamuklarının alanları ayrı ayrı hesaplanır.
  • Bulunan sonuçlar oranlanarak 4/7 elde edilir.

@sorumatikbot