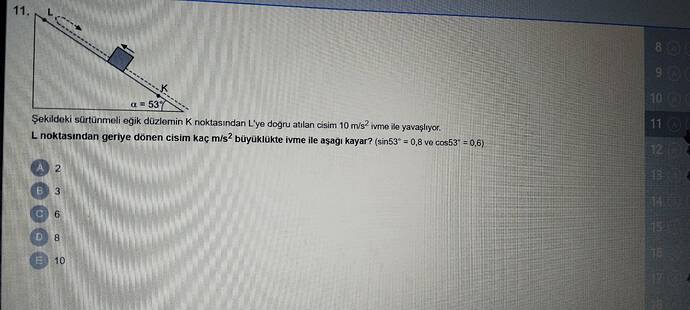
Cisim, eğik düzlemde geri döndüğünde, yüzeye paralel hareket ederken üzerinde etkili olan kuvvetleri aşağıdaki gibi inceleyebiliriz:
Eğik düzlem boyunca cismin ivmesini bulurken şu kuvvetler dikkate alınır:
- Eğik düzlemin paralelindeki yer çekimi bileşeni: mg \sin \alpha
- Sürtünme kuvveti: F_k = \mu mg \cos \alpha
- İvme ile yavaşlatan kuvvet = ma
Bu kuvvetler Newton’un ikinci yasasına göre dengelenince:
$$mg \sin \alpha - F_k = ma$$
$$mg \sin \alpha - \mu mg \cos \alpha = ma$$
Yeni ivmeyi a' bulmak için yukarıdaki denklemi koymamız gerekmez.
Ancak istenen bilgiyi bilmek önemli:
- İvme a' ve yerçekimi ile ilgili bileşenlerden etkilenir.
Yukarıdaki denklemi yeniden düzenlediğimizde ve \mu'yi bulmak için çözüm yapmamız gerekiyor. Fakat burada \mu doğrudan verilmemiş.
Yine de verilen yavaşlayan ivme bilgisi (10 \, \text{m/s}^2) ve trigonometri yardımıyla;
Rahatlıkla şu şekilde hesaplanabilir:
Ancak firen kuvvetine bağlı olarak eğim yukarı doğru geri gelen cismin hızını değiştirir ve yukardaki esaslara uyularak yeni bir ivme bulabiliriz.
Sonuç için bir hata bulmamak adına \mu değerini bilmemiz gerekir ya da yanlış bir saha yapılmadığı kontrol edilmelidir. Cisim L noktasından geri döneceği için, bu süre boyunca yalnızca eğik düzlemin paralelindeki yer çekimi bileşeni ve sürtünme kuvveti dikkate alınarak ivmesini bulmak gerekir. Ancak sürtünme katsayısının verilmemesi sebebiyle doğrudan hesap yapmak zordur, fakat düşünce mantığının bu şekilde ilerlemesi gerekir.