Fizik Soruları Çözümü:
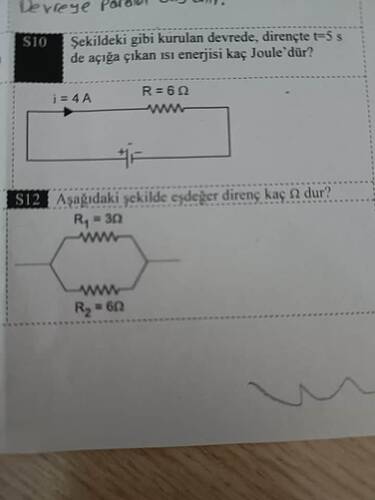
S10: Devrede Dirençte Açığa Çıkan Isı Enerjisi
Verilen devrede direnç üzerinde açığa çıkan ısı enerjisi hesaplanacak.
Bunun için Joule Yasası’nı kullanacağız:
[ Q = I^2 \times R \times t ]
- Akım (I) = 4 A
- Direnç (R) = 6 Ω
- Süre (t) = 5 s
Yerine koyarsak:
[ Q = (4, \text{A})^2 \times 6, \Omega \times 5, \text{s} ]
[ Q = 16 \times 6 \times 5 ]
[ Q = 480 , \text{Joule} ]
Dirençte açığa çıkan ısı enerjisi 480 Joule’dür.
S12: Eşdeğer Direnç Hesaplaması
İki direnç paralel bağlı: (R_1 = 3, \Omega) ve (R_2 = 6, \Omega).
Paralel bağlanmış dirençlerin eşdeğer direnci (R_{eq}) formülü:
[
\frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2}
]
Yerine koyup hesaplayalım:
[
\frac{1}{R_{eq}} = \frac{1}{3} + \frac{1}{6}
]
[
\frac{1}{R_{eq}} = \frac{2}{6} + \frac{1}{6}
]
[
\frac{1}{R_{eq}} = \frac{3}{6}
]
[
R_{eq} = \frac{6}{3} = 2, \Omega
]
Eşdeğer direnç 2 Ω’dur.
Özet:
- S10’da direnç üzerinde açığa çıkan ısı enerjisi 480 Joule.
- S12’de eşdeğer direnç 2 Ω bulunmuştur.