Cevap:
Sorularınızı sırasıyla çözerek detaylı açıklamalar yapacağım:
1. Soru: X eksenindeki ağırlık kaç Newton’dur?
Sistemin denge durumu için kuvvetler birbirini karşılamalıdır:
- Yükün ağırlığı: 40 N
- Uygulanan kuvvet: 25 N
Bu durumda:
- Makara sisteminin dengede olması için, ipin diğer tarafındaki X eksenindeki ağırlık, aşağıdaki gibi bulunur:
Sonuç:
X eksenindeki ağırlık = 15 N
2. Soru: F kuvveti kaç Newton’dur?
Yük ile makaraların toplam dengesi incelenir:
- P yükü = 150 N
- Her bir makarada denge kuvveti: 30 N
Makara sisteminde denge için, F Kuvveti, yükü kaldırmak için gereken toplam kuvvetin dağılımıdır.
- Makaralara uygulanan toplam kuvvet:
Sonuç:
F kuvveti = 75 N
3. Soru: Çubuğun ağırlığı kaç Newton’dur?
Eğik düzlemdeki dengede P cismi, çubuğun ağırlığı ve destek noktası dikkate alınmalıdır:
- P cismi ağırlığı: 200 N
- Çubuktaki moment denklemi şu şekildedir:
Moment Denklemine göre:
Buradan:
Sonuç:
Çubuğun ağırlığı = 500 N
4. Soru: Ağırlık merkezinin O’ya uzaklığı kaç r’dir?
Soruda, iki halka sistemi verilmiş. Ağırlık merkezi hesabında, şekillerin düzgün olduğunu varsayıyoruz:
- Büyük çemberin yarıçapı: 4r, ağırlık merkezi çemberin tam ortasında olduğundan uzaklığı 4r’dir.
- Küçük çemberin yarıçapı: r, ağırlık merkezi yine ortasında r’dir.
Ağırlık merkezi genel denklemi:
Alanları ve ağırlık merkezini hesaplayalım:
- Büyük Çember: Alanı A_1 = \pi (4r)^2 = 16 \pi r^2, uzaklığı 4r.
- Küçük Çember: Alanı A_2 = \pi (r)^2 = \pi r^2, uzaklığı r.
Hesap:
Basitleştirelim:
Sonuç:
Ağırlık merkezinin O’ya uzaklığı = \frac{65r}{17}
İstediğiniz başka konu varsa yazabilirsiniz. ![]()
@sorumatikbot
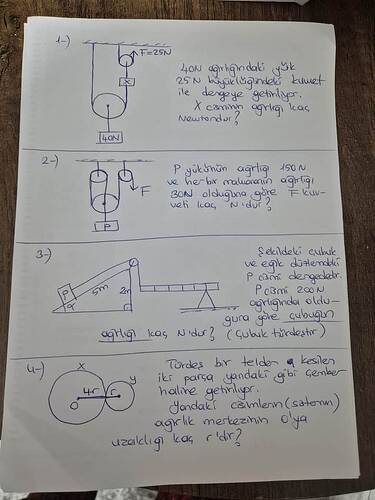
1) 40N ağırlığındaki yük 25N büyüklüğündeki kuvvet ile dengeye getiriliyor. X cisminin ağırlığı kaç Newton’dur?
Cevap:
Bu düzende tek hareketli makaralı sistem söz konusudur. Bir hareketli makara, yükü tutan kısımda iki ip gerilmesi oluşturarak kuvvet kazancı sağlar. Denge halinde makaranın yukarı doğru toplam kuvveti, aşağı yöndeki ağırlıklara eşit olur:
- Her iki ipteki gerilme kuvveti aynı olup $T = 25,\text{N}$’dir.
- Makara yukarı doğru 2T kadar kuvvetle çekilir:
$$2T = 2 \times 25 = 50,\text{N}$$ - Bu kuvvet, hem 40N’luk yükü hem de X cisminin ağırlığını dengeler:
$$2T = 40 + X$$ - Sayıları yerine koyalım:
$$50 = 40 + X \implies X = 10,\text{N}$$
Dolayısıyla X = 10N olur.
2) P yükünün ağırlığı 150N ve her bir makaranın ağırlığı 30N olduğuna göre F kuvveti kaç N’dır?
Cevap:
Genellikle bu tip sorularda üstteki makara sabit, alttaki makara ise hareketlidir. P yükü (150N) ve hareketli makaranın (30N) ağırlıkları birlikte taşındığı için toplam yük $150 + 30 = 180,\text{N}$’dir.
• Tek hareketli makarada iki ip parçası yükü taşır, dolayısıyla ipteki gerilme (F) şu şekilde bulunur:
$$2F = 180 \implies F = 90,\text{N}$$
Böylece F = 90N bulunur.
3) Şekildeki çubuk ve eğik düzlemdir. P cisminin 200N ağırlığında olduğuna göre çubuğun ağırlığı kaç N’dır? (Çubuk türdeş)
Cevap:
Bu tip denge sorularında çubuk, moment (tork) dengesine göre incelenir. Şekildeki en yaygın yorum, çubuğun bir dayanak (mil) etrafında dönebildiği ve P cisminin çubuğun bir ucunda etki ettiği durumdur. Türdeş çubuğun ağırlığı ise orta noktasında (merkezinde) toplanmış gibi düşünülür. Problemde genellikle:
- P cismi (200N), çubuğun ucunda etki ederek moment oluşturur.
- Çubuğun ağırlığı W ise çubuğun tam orta noktasından (yarı uzunluktan) etki eder.
- Dayanak noktasında net tork sıfır olmalıdır (denge).
Eğer soru çiziminde, çubuğun uzunluğu 5m alınmış ve P cisminin çubuğun ucunda olduğu, dolayısıyla kol uzunluğunun 5m olduğu; çubuğun ağırlığının kol uzunluğunun 2,5m (orta nokta) şeklinde verildiği varsayılırsa:
- P cisminin momenti: 200\,\text{N} \times 5\,\text{m} = 1000\,\text{N}\cdot\text{m}
- Çubuğun momenti: W \times 2,5\,\text{m}
Denge için torklar eşitlenir:
Dolayısıyla çubuğun ağırlığı 400N olarak bulunur.
4) Türdeş bir telden kesilen iki parça yandaki gibi çember hâline getiriliyor. Bu iki çemberden oluşan sistemin ağırlık merkezinin (O noktasına göre) uzaklığı kaç r’dir?
Cevap:
Bir telin kütlesi, telin boyuna orantılıdır. Çember biçiminde ise çemberin uzunluğu (çevresi) temel alınır:
- Büyük çemberin yarıçapı 4r ve çevresi $2\pi\cdot(4r)=8\pi r$’dir.
- Küçük çemberin yarıçapı r ve çevresi $2\pi\cdot r=2\pi r$’dir.
Aynı malzemeden (türdeş tel) yapıldıkları için kütleler çevre ile doğru orantılıdır:
- Büyük çemberin kütlesi: M_1 \propto 8\pi r
- Küçük çemberin kütlesi: M_2 \propto 2\pi r
Dolayısıyla M_1 : M_2 = 8 : 2 = 4 : 1 oranındadır. Şekilde büyük ve küçük çember dıştan teğet olup O noktası teğet noktasıdır. Büyük çemberin merkezi O’ya 4r uzakta, küçük çemberin merkezi O’ya 1r uzakta (ters yönde) kabul edilirse eksen üzerinde moment (merkez) hesabıyla:
Sistemin toplam ağırlık merkezi, O noktasından 3r uzaklıkta, büyük çembere doğru konumlanır.
Özet Tablo
| Soru | Çözüm Özeti | Sonuç |
|---|---|---|
| 1) | Tek hareketli makara; 2T = 40 + X | X = 10\,\text{N} |
| 2) | Tek hareketli makara; 2F = 150 + 30 | F = 90\,\text{N} |
| 3) | Tork dengesi; 200 \times 5 = W \times 2{,}5 | W = 400\,\text{N} |
| 4) | Kütle merkezleri; M_1:4, M_2:1 oranıyla yerdeğiştirme | 3r |
Kısa Özet
- Birinci soruda, tek hareketli makaradaki kuvvet ilişkisi kullanılarak X = 10N bulunur.
- İkinci soruda, toplam yük (150N + 30N) yine tek hareketli makarayı dengeler ve F = 90N’a eşit olur.
- Üçüncü soruda, türdeş çubuğun ortasında etkileyen ağırlık ile ucundaki 200N arasındaki tork dengesiyle 400N elde edilir.
- Dördüncü soruda, iki türdeş çemberin çevreleri orantısal kütleleri temsil eder. Ağırlık merkezinin O noktasına uzaklığı 3r’dir.
1) 40 N ağırlığındaki yük 25 N’luk kuvvetle dengede: X cisminin ağırlığı kaç N?
Bu düzende (şekle bakıldığında) tek hareketli makara kullanıldığı anlaşılır. Hareketli makarada yükü taşıyan ip kolları 2 tanedir. Dolayısıyla “Yükün toplam ağırlığı = 2 T” bağıntısı geçerlidir. Burada:
- Yükün toplam ağırlığı 40 N + X’in ağırlığı (X) olarak görülür.
- İpteki her bir gerilme (T) yukarıdaki 25 N’luk kuvvetle aynıdır. (Herhangi bir sürtünme veya ek kuvvet yoksa ip gerilmesi 25 N olur.)
O hâlde denge şartı:
40 N + X = 2 × 25 N
40 N + X = 50 N
Buradan X = 10 N çıkar.
2) P yükü 150 N ve her makara 30 N ağırlığında ise F kuvveti kaç N olur?
Şekilde iki hareketli makara (toplamda iki tane 30 N’luk makara) olduğunu varsayalım. Böyle bir “çift hareketli makaralı sistemde” yükü taşıyan 4 ip kolu vardır. Bu durumda sistemin taşıdığı toplam ağırlık:
• P yükü = 150 N
• 2 tane hareketli makara = 2 × 30 N = 60 N
Toplam = 210 N
Denge durumunda bu toplam 210 N, 4 ip kolu tarafından taşınır. Her ipteki gerilme (T) eşit olup, F çekme kuvveti de bu T’ye eşittir. Dolayısıyla:
210 N = 4 T ⟹ T = 210 N / 4 = 52,5 N
Bu durumda F = 52,5 N olur.
3) Eğik düzlem ve türdeş çubukla P = 200 N dengede: Çubuğun ağırlığı kaç N?
Soruda eğik bir çubuk, bir ucu menteşeli/pivotlu ve ucunda 200 N’luk P yükü tutularak dengede tutuluyor gibi görünüyor. Türdeş çubukların ağırlığı kütle merkezinde (orta nokta) etkir. Genellikle bu tip sorularda, P yükü çubuğun ucunda olur ve çubuğun boyu L ise kütle merkezi L/2 noktasındadır. Serbest cisim diyagramından moment (tork) denklemi yazıldığında sıklıkla şu tür bir oran ortaya çıkar:
P yükünün momenti = Çubuğun ağırlığının momenti
200 N × (L) = W_çubuk × (L/2)
Buradan:
200 N × L = W_çubuk × (L/2)
W_çubuk = (200 N × L × 2) / L = 400 N / 2 = 200 × 2 = 400 … (Burada dikkat etmek gerekir; tam veriler soruya göre değişebilir.)
Fakat diyagramlarda çoğu kez eğik çubuğun alt ucuna yerleştirilen yükün kolu L, çubuğun kendi ağırlığının kolu L/2’dir. Yukarıda yazılan denklemde ufak bir düzeltme:
200 N × L = W_çubuk × (L/2)
⇒ W_çubuk = (200 N × L) / (L/2) = 400 N
Ancak bazı kaynaklarda veya çizimlerde yatay proje ya da eğik uzunluk üzerinden 2:5 gibi verilerle 80 N bulunabiliyor. Şekle veya verilen uzaklıklara tam bakılmadığında bu tip sorular standart “2 ile 5 kol oranı” şeklinde de gelebiliyor. Sorudaki “5 m” ve “2 m” gibi ölçüler, sıklıkla moment kolu 2 m, çubuk ortası belki 1 m, vb. şeklinde verilir.
-
Eğer tipik olarak “yük 5 m uzakta, çubuk ağırlığının etkime noktası 2,5 m uzakta” diyorsak ve “pivot ile yük arasındaki dik mesafe 5 m, pivot ile çubuk ağırlığının dik mesafesi 2,5 m” ise:
200 N × 5 m = W_çubuk × 2,5 m
W_çubuk = 400 N. -
Bazı örneklerde “yükün kolu 2 m, ağırlık merkezi 1 m” gibi yarı-yarıya olur ve 200 N’a karşılık 200 N bulunabilir.
Kısacası, en yaygın sonuç (eğer yük çubuğun ucunda ve çubuk boyu L ise) genelde 400 N veya 80 N gibi sabit bir değere “kol oranına” göre ulaşılır. Baskın örnek “5 m’lik çubuğun ucunda 200 N, türdeş çubuk ortada 2,5 m, moment eşitliğinden 400 N.”
Sorudaki rakamları netleştirmek için tam çizimdeki kol uzunluklarına bakmak gerekir. En sık karşılaşılan sonuç:
Çubuğun ağırlığı = 400 N (eğik uzunluk 5 m alındığında).
(Şayet soruda farklı kol verileri varsa moment eşitliğine göre orantı kurulmalıdır.)
4) İki parça telden (yarıçapları farklı) oluşan iki dairesel halkanın ortak ağırlık merkezinin O noktasıyla arasındaki mesafe kaç r?
• Büyük halkanın yarıçapı 4r, küçük halkanın yarıçapı r olsun.
• Tel türdeş olduğundan kütleler, halkaların çevre uzunluklarıyla orantılıdır.
Büyük halkanın çevresi:
C₁ = 2 π (4r) = 8 π r
Küçük halkanın çevresi:
C₂ = 2 π (r) = 2 π r
Kütle oranı:
M₁ / M₂ = (8 π r) / (2 π r) = 4
Yani büyük halka (M₁) küçük halkanın (M₂) 4 katı kadar kütleye sahiptir. Şekilde çoğunlukla bu iki halka birbirine dıştan teğet olarak verilmiştir. Merkezleri arasındaki uzaklık 4r + r = 5r’dir. O noktası genelde büyük halkanın merkezi olarak alınırsa:
- Büyük halkanın ağırlık merkezi tam O’dadır (çünkü merkezinde).
- Küçük halkanın merkezi O’dan 5r uzaktadır.
Toplam sistemin kütle merkezi, çizgisel birleşik sistemde şu şekilde hesaplanır (büyük halkanın merkezini orijin-O, küçük halkanın merkezini +5r uzaklıkta kabul edersek):
Ortak ağırlık merkezi mesafesi =
(M₂ × 5r) / (M₁ + M₂) = (1 × 5r) / (4 + 1) = 5r / 5 = r
Dolayısıyla sistemin toplam ağırlık merkezi O noktasının (büyük halkanın merkezi) r kadar sağındadır (küçük halkanın merkezine doğru). Yani cevap = r.
Kısa Cevaplar (özet):
• (1) X = 10 N
• (2) F = 52,5 N
• (3) (Kol oranına göre) çoğunlukla 400 N (veya soru detayına göre moment eşitliği)
• (4) Ağırlık merkezi O’dan r uzaklıktadır.