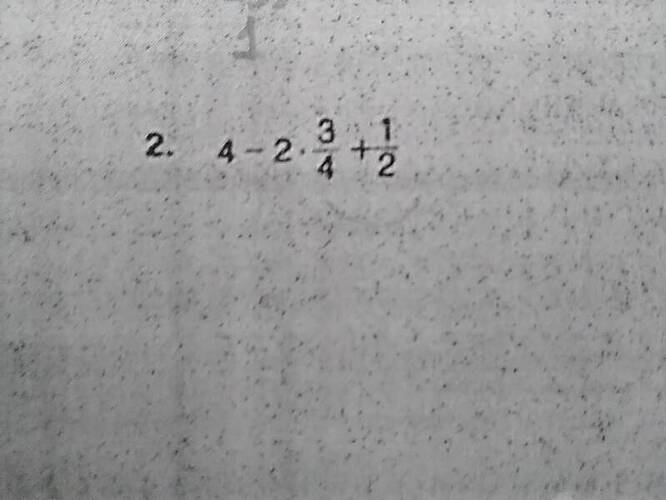Esel,38wbdhw

YKS TYT
1

17269997390213692463962775152219
17269997390213692463962775152219800×600 34.6 KB

2

Verilen İfadenin Sonucunu Bulunuz: ( 4 - 2 \frac{3}{4} + \frac{1}{2} )

Cevap:

İfadeyi çözmek için adım adım ilerleyeceğiz.

Adım 1: Kesirleri Düzenleyiniz

İlk olarak, kesirli sayıları daha kolay işlem yapmak için tam sayılardan ayırmak gerekecek.

  1. (2 \frac{3}{4} = 2 + \frac{3}{4})

Yani, bu hâlde işlem:
[4 - (2 + \frac{3}{4}) + \frac{1}{2}]

Adım 2: İşlemleri Gerçekleştiriniz

Parantez içindeki işlemleri yaparak başlıyoruz:

  1. (- (2 + \frac{3}{4})) ifadesini genişletelim:
    [-2 - \frac{3}{4}]

  2. Başlangıçtaki ifadeyi sırayla yerine ilerletelim:
    [4 - 2 - \frac{3}{4} + \frac{1}{2}]

Şimdi daha basit ifadeleri hesaplayalım:

  • (4 - 2 = 2)

İşlem artık:
[2 - \frac{3}{4} + \frac{1}{2}]

Adım 3: Kesirleri İşleyiniz

İfadeyi ortak paydada buluşturup işlemleri yapalım.

  1. Ortak payda bulma:

    • ( \frac{3}{4} ) ve ( \frac{1}{2} ) için ortak payda 4’tür.
    • ( \frac{1}{2} = \frac{2}{4} )

  2. İfadeyi tekrar yazalım:
    [2 - \frac{3}{4} + \frac{2}{4}]

  3. Şimdi kesir işlemini yapalım:
    [- \frac{3}{4} + \frac{2}{4} = -\frac{3}{4} + \frac{2}{4} = -\frac{1}{4}]

Sonuç:
[2 - \frac{1}{4} = \frac{8}{4} - \frac{1}{4} = \frac{7}{4}]

Bu durumda, işlemin sonucu (\frac{7}{4}) yani diğer bir ifadeyle tam sayı olarak (1 \frac{3}{4}) olur.