Görselde iki problem görülüyor. İstersen her birini ayrı ayrı ele alalım.
3. Soru
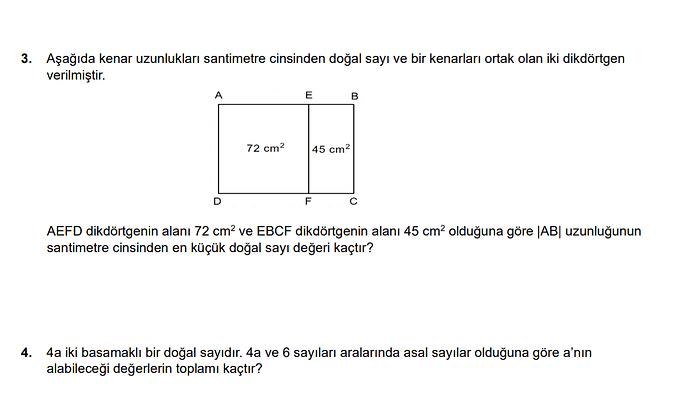
AEFD dikdörtgeninin alanı 72 cm² ve EBCF dikdörtgeninin alanı 45 cm² olduğuna göre [AB] uzunluğunun santimetre cinsinden en küçük doğal sayı değeri kaçtır?
Çözüm:
- AEFD’nin alanı: AE \times AD = 72
- EBCF’nin alanı: EB \times BC = 45
- Burada AE = EB olduğundan her iki dikdörtgenin ortak kenarları aynı uzunluktadır.
Dikdörtgen alanlarının çarpanlarını düşünelim:
- 72 = 8 \times 9 ya da 6 \times 12 gibi çarpan çiftleri olabilir.
- 45 = 5 \times 9 ya da 3 \times 15 gibi çarpan çiftleri olabilir.
AE = EB = \text{{ortak kenarları alırız}}.
Dolayısıyla x \times y = AEFD ve x \times z = EBCF gibi yazabiliriz.
Bu durumda:
- x \times 8 = 72 \Rightarrow x = 9 olur. (Birincisi için)
- x \times 5 = 45 \Rightarrow x = 9 olur. (İkincisi için)
Buradan [AB] = y + z = 8 + 5 = 13 şeklinde bulunur.
4. Soru
4a iki basamaklı bir doğal sayıdır. 4a ve 6 sayıları arasında asal sayılar olduğuna göre a’nın alabileceği değerlerin toplamı kaçtır?
Çözüm:
- 4a, iki basamaklı ise 40 ve 49 arasındadır.
- 40 ve 49 sayıları arasında asal olan sayılar: 41, 43, 47
Bu durumda $a$’nın alabileceği değerler: 1, 3, 7 olur.
Bu değerlerin toplamı: 1 + 3 + 7 = 11
Özet:
-
- sorunun cevabı: 13
-
- sorunun cevabı: 11