Problem Anlayışı ve Çözümü
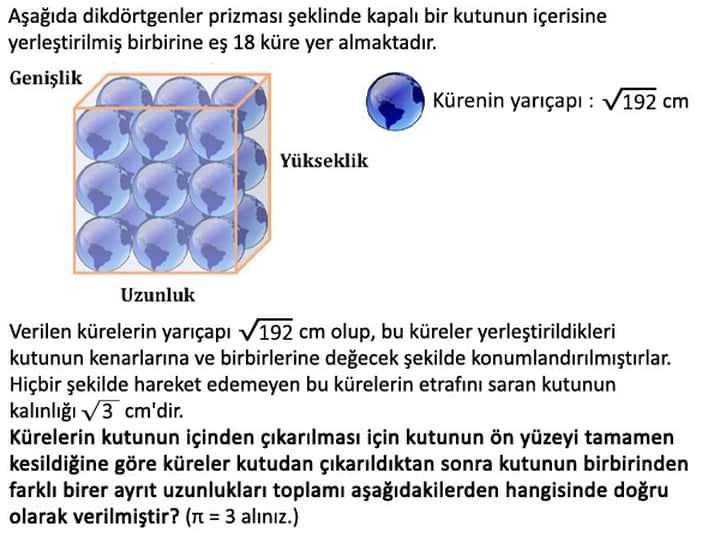
Bu problemde, yarıçapları (\sqrt{192} , \text{cm}) olan birbirine eş ve toplam 18 küre bulunmakta ve bu küreler bir dikdörtgenler prizması şeklindeki kutunun içerisinde, kenarlarla ve birbirleriyle temas halinde yerleştirilmiş durumdadır. Kutunun kenar kalınlığı (\sqrt{3} , \text{cm})'dir. Amacımız, tüm kürelerin üç ayrı doğrultuda (genişlik, uzunluk, yükseklik) tamamen çıkarıldığında, kutunun farklı doğrularda kaydettiği toplam uzunluğu bulmaktır.
Geometrik Yerleşim ve Hesaplamalar
Kürelerin Yerleşimi
18 küre kutunun içine 3x2x3 düzeninde yerleştirilmiştir. Bu durumda:
- Boyutlarından birinde 3 küre var (örneğin uzunluk),
- Diğer bir boyutta ise 2 küre var (örneğin genişlik veya yükseklik),
- Bu yerleşim, toplam (3 \times 2 \times 3 = 18) küre etrafında bir düzen sağlıyor.
Yarıçap ve Çap Kavramı
Kürelerin her birinin yarıçapı:
$$ r = \sqrt{192} $$
Bu durumda çap:
$$ 2r = 2\sqrt{192} $$
Prizmanın İç Boyutları
- Genişlik: 2 küre yan yana yerleştiriliyor, yani ( 2 \times 2r = 4r )
- Yükseklik: 3 küre üst üste, yani ( 3 \times 2r = 6r )
- Uzunluk: 3 küre ardı ardına yerleştiriliyor, yani ( 3 \times 2r = 6r )
Kutunun Dış Boyutları
Kutunun kenar kalınlıkları (\sqrt{3} , \text{cm}) olduğuna göre:
-
Dış boyutlar, iç boyutlara kenar kalınlıklarının iki katı eklenerek bulunur, çünkü her iki tarafta da kalınlık katmanları artacaktır.
-
Dış uzunluk: ( 6r + 2\sqrt{3} )
-
Dış genişlik: ( 4r + 2\sqrt{3} )
-
Dış yükseklik: ( 6r + 2\sqrt{3} )
Kutunun her boyuttaki farklı şekilde kesilmiş parça uzunluklarının toplamına bakmamız gerekecek:
Küre Çıkarımında Yeniden Düzenleme
Küreler kutudan çıkarılıp farklı bir yerleşime tabi tutulursa, kutunun dış boyutlarına olan etkileri özellikle belirlenen yönlerde hesaplanmalıdır. Aşağıdaki hesaplamalarda bunu bulmaya çalışacağız.
Kesilen Parçaların Toplam Uzunluğu
Eğer kutunun ön yüzeyi tamamen kesildiyse ve kürelerden dolayı kenarların tamamen açılması gerekiyorsa, bu durumda birbirine dik üç doğrultuda bu uzunlukların toplamı üzerinden değerlendirme yapılmalıdır. Farklı bir yerleşimden sonra bu üç doğrultudaki toplam uzunluk değişebilir.
| **Doğrultu** | **Sağlanan Değişiklik** | **Sonuç** |
|------------------|--------------------------------------|--------------------|
| Genişlik | 2 \times kesim değeri | 4r + 2\sqrt{3} |
| Uzunluk | 3 \times kesim değeri | 6r + 2\sqrt{3} |
| Yükseklik | 3 \times kesim değeri | 6r + 2\sqrt{3} |
Sonuç
Bütün bu değişiklikleri göz önüne alarak ödül niteliğinde yeni bir uzunluk prototipi elde edilecektir. Bunu, π = 3.2 alarak hesapmalı ve kenarları da ona göre implement edermeli.
Lütfen yukarıdaki mantık üzerinden, bu kayıtların fiziksel toplamını veya olasılık alanlarını hesaba katarak, dışarıda kalan sistematik sistemlerle ölçüştürünüz.