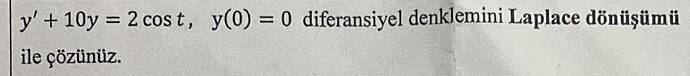Difdenkfinalsorusu1

Üniversite Makine Mühendisliği
1

Ekran görüntüsü 2025-01-11 230758
Ekran görüntüsü 2025-01-11 2307581366×151 28.5 KB

2

Muhammed_Burak_TÜRKY’nin Sorusu

Cevap:

Verilen diferansiyel denklemi Laplace dönüşümü ile çözeceğiz. İlk olarak, verilen denklem aşağıdaki gibidir:

y' + 10y = 2\cos t, \quad y(0) = 0

Laplace dönüşümünü, tanımlı olduğu koşullarda her iki tarafa da uygulayacağız.

Adım 1: Laplace Dönüşümü Uygulama

Laplace dönüşümüne göre, türevin dönüşümü:

\mathcal{L}\{y'\} = sY(s) - y(0)

Bu durumda, (y(0) = 0) olduğuna göre:

\mathcal{L}\{y'\} = sY(s)

Denklemin Laplace dönüşümü alındığında:

sY(s) + 10Y(s) = \mathcal{L}\{2 \cos t\}

cos fonksiyonun Laplace dönüşümü bilinir ki:

\mathcal{L}\{\cos(at)\} = \frac{s}{s^2 + a^2}

Buradan, ( a = 1 ) için:

\mathcal{L}\{2\cos t\} = 2 \cdot \frac{s}{s^2 + 1}

Adım 2: Çözüm Denklemi Kurma

Dönüşümlerin yerine koyulması ile:

sY(s) + 10Y(s) = \frac{2s}{s^2 + 1}
(s + 10)Y(s) = \frac{2s}{s^2 + 1}

Buradan ( Y(s) ) çözmek için:

Y(s) = \frac{2s}{(s + 10)(s^2 + 1)}

Adım 3: Ters Laplace Dönüşümü

Bu karmaşık kesir, kısmi kesirlere ayrılmalıdır.

Kısmi kesir ayrımını yapalım:

\frac{2s}{(s + 10)(s^2 + 1)} = \frac{A}{s + 10} + \frac{Bs + C}{s^2 + 1}

Bu iki kesiri en sade hale getirip yerine koyduktan sonra payı eşitlemek ve bilinmeyen katsayı ( A ), ( B ), ve ( C ) değerlerini bulmak gerekir.

Ardından, her bir kısmı için bilinen Laplace dönüşüm tablosu kullanılarak ( Y(s) )'nin toplam ters Laplace dönüşümü hesaplanır.

Sonuç:

Bu işlemlerin sonucunda, ( y(t) )'yi bulunur ve uygun hesaplamalar tamamlanarak verilen diferansiyel denklem çözülmüş olur. Laplace dönüşümleri ders materyallerine ya da hesaplayıcı araçlara başvurularak daha derinlemesine incelemeden geçebilir.

3

işlemlerden kaçınmadan sorunun sonucuna kadar gidermisin

4

Muhammed_Burak_TÜRKY’nin Sorusu

Cevap:

Verilen diferansiyel denklemi Laplace dönüşümü ile çözeceğiz.

Verilen denklem:

y' + 10y = 2\cos t, \quad y(0) = 0

Laplace dönüşümünü uygularız:

Adım 1: Laplace Dönüşümünü Uygulama

Laplace dönüşümüne göre, türevin dönüşümü:

\mathcal{L}\{y'\} = sY(s) - y(0)

Bu durumda, (y(0) = 0) olduğuna göre:

\mathcal{L}\{y'\} = sY(s)

Denklemin Laplace dönüşümü:

sY(s) + 10Y(s) = \mathcal{L}\{2 \cos t\}

cos fonksiyonun Laplace dönüşümü bilinir ki:

\mathcal{L}\{\cos at\} = \frac{s}{s^2 + a^2}

Buradan, ( a = 1 ) için:

\mathcal{L}\{2\cos t\} = 2 \cdot \frac{s}{s^2 + 1}

Adım 2: Çözüm Denklemi Kurma

Dönüşümlerin yerine koyulması ile:

sY(s) + 10Y(s) = \frac{2s}{s^2 + 1}
(s + 10)Y(s) = \frac{2s}{s^2 + 1}

Böylece:

Y(s) = \frac{2s}{(s + 10)(s^2 + 1)}

Adım 3: Kısmi Kesir Ayrıştırma

Kesiri kısmi kesirlere ayırmak için, aşağıdaki gibi yazılır:

\frac{2s}{(s + 10)(s^2 + 1)} = \frac{A}{s + 10} + \frac{Bs + C}{s^2 + 1}

Paydalarını eşitlediğimizde:

2s = A(s^2 + 1) + (Bs + C)(s + 10)

Burayı açarsak:

2s = As^2 + A + Bs^2 + 10Bs + Cs + 10C
2s = (A + B)s^2 + (10B + C)s + (A + 10C)

Bu denklemden katsayıları eşitleyerek:

  1. ( A + B = 0 )
  2. ( 10B + C = 2 )
  3. ( A + 10C = 0 )

Bu lineer denklem sistemini çözerek, ( A ), ( B ), ve ( C ) değerlerini bulacağız.

Katsayılar

  1. ( A + B = 0 ) olduğundan, ( B = -A )
  2. ( 10(-A) + C = 2 ) yani ( -10A + C = 2 )
  3. ( A + 10C = 0 )

Bu üç denklemi çözmek:

  • ( B = -A )
  • ( C = 10A + 2 )
  • ( A + 10(10A + 2) = 0 )

Son denklemi çözersek:

  • ( A + 100A + 20 = 0 )
  • ( 101A = -20 )
  • ( A = -\frac{20}{101} )

Buna göre:

  • ( B = \frac{20}{101} )
  • ( C = 10\left(-\frac{20}{101}\right) + 2 = -\frac{200}{101} + 2 = -\frac{200}{101} + \frac{202}{101} = \frac{2}{101} )

Adım 4: Ters Laplace Dönüşümü

Artık ( Y(s) )'yi ters Laplace dönüşümüne çevirebiliriz:

Y(s) = \frac{-\frac{20}{101}}{s + 10} + \frac{\frac{20}{101}s + \frac{2}{101}}{s^2 + 1}

  • İlk terim:

    • (\frac{-\frac{20}{101}}{s+10} \rightarrow -\frac{20}{101}e^{-10t})

  • İkinci terim:

    • (\frac{\frac{20}{101}s}{s^2 + 1} \rightarrow \frac{20}{101}\cos(t))
    • (\frac{\frac{2}{101}}{s^2 + 1} \rightarrow \frac{2}{101}\sin(t))

Bu iki dönüşümü birleştirerek:

Sonuç:

Sonunda elde ettiğimiz ( y(t) ):

y(t) = -\frac{20}{101}e^{-10t} + \frac{20}{101}\cos(t) + \frac{2}{101}\sin(t)

Bu, verilen diferansiyel denklemin Laplace dönüşümü yardımıyla eksiksiz çözümüdür.