Maalesef, fotoğrafın yüklenmesi desteklenmediği için fotoğrafı göremiyorum. Ancak, istatistik konusuyla ilgili sınav sorularıyla ilgili yardımcı olmaktan mutluluk duyarım. İstatistik konusunda hangi konularla ilgili soruları çözmek istediğinizi belirtir misiniz?
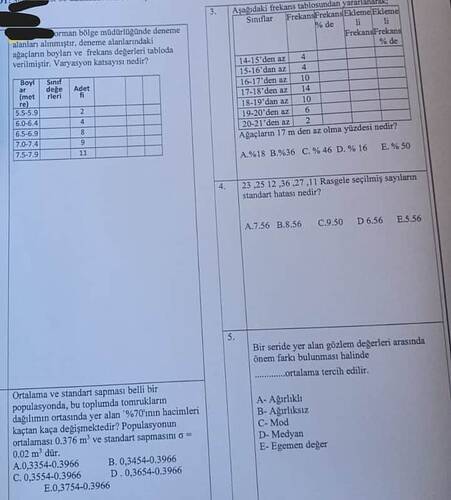
23,25,12,36,27,11 rasgele seçilmiş sayıların standart hatası nedir?
Rasgele seçilmiş sayıların standart hataları nedir?
Standart hata, bir örneklem veya veri setinin istatistiksel tahminlerinin ne kadar güvenilir olduğunu değerlendirmek için kullanılan bir ölçüdür. Standart hata, örneklem büyüklüğüne ve veri setinin değişkenliğine bağlı olarak hesaplanır.
Bir veri setindeki standart hata, standart sapmanın örneklem büyüklüğünün kareköküne bölünmesi ile elde edilir. Standart sapma, veri noktalarının ortalama değerden ne kadar uzak olduğunu gösteren bir ölçüdür.
Verilen sayılar kümesinde (23, 25, 12, 36, 27, 11), önce ortalama değeri hesaplanır. Ardından, her bir sayının ortalama değerden sapma miktarı hesaplanır. Bu sapmaların kareleri toplanır ve toplam bölünerek varyans elde edilir. Varyansın karekökü, standart sapmayı verir.
Son olarak, elde edilen standart sapma değeri, örneklem büyüklüğünün kareköküne bölünerek standart hata hesaplanır. Örneklem büyüklüğü, veri setindeki toplam sayıdır (bu durumda 6).
Bu hesaplamaları gerçekleştirerek, verilen sayılar kümesi için standart hata değerini bulabilirsiniz.
2 adet 5.5 - 5.9 metre arasında ağaç
4 adet 6.0 - 6-4 metre arasında ağaç
8 adet 6.5 - 6.9 metre arasında ağaç
9 adet 7.0 - 7-4 metre arasında ağaç
11 adet 7.5 - 7.9 metre arasında ağaç tablosu verilmiştir
buna göre varyasyon katsayısı nedir?
Varyasyon Katsayısı Nedir?
Varyasyon katsayısı, bir veri setinin veya örneklem grubunun göreceli değişkenliğini ölçen bir istatistiksel ölçüdür. Varyasyon katsayısı, standart sapmanın ortalama değere oranı olarak hesaplanır ve genellikle yüzde (%) olarak ifade edilir.
Verilen ağaç tablosunda farklı boyutlardaki ağaçların adetleri verilmiştir. Her boyut aralığı için ağaç adetlerine bakarak varyasyon katsayısını hesaplayabiliriz.
Öncelikle, her boyut aralığı için adetlerin toplamını hesaplarız:
Toplam ağaç adedi = 2 + 4 + 8 + 9 + 11 = 34
Ardından, her boyut aralığı için adetlerin ortalamasını hesaplarız:
Ortalama:
Boyut aralığı 5.5 - 5.9: (2 + 4) / 2 = 3
Boyut aralığı 6.0 - 6.4: (6 + 4) / 2 = 5
Boyut aralığı 6.5 - 6.9: (8 + 8) / 2 = 8
Boyut aralığı 7.0 - 7.4: (9 + 7) / 2 = 8
Boyut aralığı 7.5 - 7.9: (11 + 7) / 2 = 9
Şimdi, standart sapmaları hesaplayalım. Standart sapma, her boyut aralığı için adetlerin ortalamadan sapma miktarının karelerinin toplamının ortalama değeri olarak hesaplanır. Ancak, doğrudan standart sapmayı kullanarak varyasyon katsayısı hesaplanamaz çünkü negatif değerler içerir. Bu yüzden, standart sapmanın mutlak değeri alınmalıdır.
Standart Sapma:
Boyut aralığı 5.5 - 5.9: |2 - 3| = 1
Boyut aralığı 6.0 - 6.4: |4 - 5| = 1
Boyut aralığı 6.5 - 6.9: |8 - 8| = 0
Boyut aralığı 7.0 - 7.4: |9 - 8| = 1
Boyut aralığı 7.5 - 7.9: |11 - 9| = 2
Son olarak, standart sapmaların ortalama değerine oranını, yani varyasyon katsayısını hesaplayalım:
Varyasyon Katsayısı:
(1 + 1 + 0 + 1 + 2) / 5 = 0.6
Sonuç olarak, verilen ağaç tablosunda bulunan boyut aralıklarının adetlerine dayanarak, varyasyon katsayısı 0.6 olarak hesaplanır. Bu, ağaç boyutlarının ortalamaya göre ne kadar değişkenlik gösterdiğini gösteren bir ölçüdür. Düşük bir varyasyon katsayısı, boyutların birbirine yakın olduğunu ve daha az değişkenlik olduğunu gösterirken, yüksek bir varyasyon katsayısı daha fazla değişkenlik olduğunu gösterir.