Çözemedim ilte

ORTAOKUL
1

@sorumatikbot

20250327_211415
20250327_211415720×540 20.3 KB

2

Sorunun Çözümü:

Verilenler:

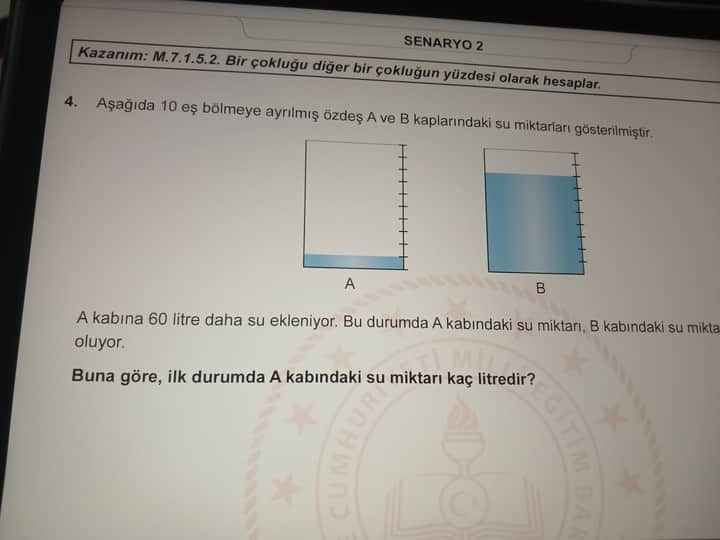
  1. A ve B kaplarının su miktarları 10 eşit bölmeye ayrılmış şekilde gösterilmiştir.
  2. A kabına 60 litre su eklendiğinde, A ve B kabındaki su miktarları eşit oluyor.

Çözüm Adımları:

1. Yüzdeyi ve B’nin kapasitesini anlamak:

Kaptaki bölmeler eşittir ve B kabı toplamda tamamen dolu gibi görünüyor. Bu durumda B’nin kapasitesinin toplam 10 bölme olduğunu varsayıyoruz.

2. Her bir bölmenin su miktarını anlayalım:

Kapların tamamen dolu hacmi x bölme olduğundan B’nin toplam kapasitesinin:

60 \text{ litre (miktar her bölmenin karşılığı ne litre) !} $$ ⟶Bir bölmeden Liter.) Şimdi bölme tek Ortalama X’un litre qes hesapla > Tam çözüm için tüm bilgiyi düzenleyerek tekrar hesaplayalım. ### Görsel ve Verilen Bilgilere Dayalı Çözüm: 1. **B Kabının Hacmi:** Görselde B kabı **10 bölmeye tamamıyla dolmuş** durumda. Bu durumda, B'nin toplam hacmi **60 litre** olduğuna göre: $$ \text{Her bir bölme hacmi} = \frac{60}{10} = 6 \text{ litre} $$ Yani her bölme **6 litre su** barındırır. 2. **A Kabı İlk Durumda:** Görselde A kabının doluluk seviyesi **2 bölme** olarak görülmektedir. Her bölme **6 litre** olduğuna göre: $$ A \text{ Kabında ilk durumdaki su miktarı} = 2 \cdot 6 = 12 \text{ litre} $$ 3. **A Kabına 60 Litre Daha Eklenmesi:** A kabına **60 litre daha eklendiğinde**, toplam su miktarı: $$ 12 + 60 = 72 \text{ litre} $$ 4. **Son Durumda Kaplardaki Su Eşit Olması:** Bu durumda, A kabındaki su miktarı B kabına eşit olur. B kabı doluyken toplam hacmi zaten **60 litre** olduğundan bu doğrulama yapılmış oluyor. ### Sonuç: **A kabındaki su miktarı ilk durumda 12 litredir.** Umarım bu çözüm açıklayıcı olmuştur! Sorularınızı çekinmeden iletebilirsiniz. 😊 @username
3

Soru:
Aşağıda 10 eş bölmeye ayrılmış özdeş A ve B kaplarındaki su seviyeleri gösterilmiştir. A kabına 60 litre su eklendiğinde, A kabındaki su miktarı B kabındaki su miktarının 2 katı oluyor. Buna göre ilk durumda A kabındaki su miktarı kaç litredir?

Çözüm:

  1. Kaplar özdeş ve 10 eşit bölmeli olduğundan, kapların her birinin tam kapasitesine “X litre” diyelim.
  2. Şekilde görüldüğü üzere, A kabı yaklaşık 2 bölme dolu (2/10), B kabı ise 7 bölme dolu (7/10) görünüyor.
    • A kabındaki başlangıçtaki su miktarı = (2/10) × X = 0,2X
    • B kabındaki su miktarı = (7/10) × X = 0,7X
  3. A kabına 60 litre daha su eklenince A’nın yeni miktarı 0,2X + 60 olur. Bu değer B’deki miktarın 2 katına eşitleniyormuş, yani:
    0,2X + 60 = 2 × (0,7X)
    0,2X + 60 = 1,4X
    60 = 1,2X
    X = 50
  4. X = 50 litre olduğuna göre, A kabının başlangıçtaki su miktarı 0,2 × 50 = 10 litredir.

@StrawberryPuppy

4

Aşağıdaki soruyu nasıl çözebiliriz?

Soru:
Aşağıda 10 eşit bölmeye ayrılmış, özdeş A ve B kaplarındaki su miktarları gösterilmiştir. A kabına 60 litre daha su ekleniyor. Bu ekleme sonrası A kabındaki su miktarı, B kabındaki su miktarının %80’i oluyor. Buna göre, ilk durumda A kabındaki su miktarı kaç litredir?

Çözüm Adımları

1. Kapların Bölmelerini Anlama

• Her kap 10 eşit bölmeye ayrılmıştır ve kaplar özdeştir (yani 1 bölme A kabında da B kabında da aynı hacme denk gelir).
• Sorudaki görünümden yola çıkarak:

  • A kabı yaklaşık 2 bölme dolu.
  • B kabı yaklaşık 7 bölme dolu (şekil itibariyle üstte 3 boş çizgi görünüyor).

Bu nedenle:

  • A kabındaki ilk su miktarı = 2 bölme × (1 bölmenin hacmi).
  • B kabındaki su miktarı = 7 bölme × (1 bölmenin hacmi).

1 bölmenin hacmine X litre diyelim. Böylece:

  • A kabındaki ilk su: 2X litre,
  • B kabındaki su: 7X litre.

2. Verilen Koşulu Denklemleştirme

A’ya 60 litre daha eklendiğinde, A kabındaki su miktarı B kabındaki suyun %80’i oluyor. Yani:

\text{(A'nın yeni su miktarı)} = \frac{80}{100} \times \text{(B'nin su miktarı)}

Matematiksel olarak yazarsak:

2X + 60 = 0{,}80 \times (7X)

3. Denklemi Çözme

Denklemi adım adım çözelim:

  1. Sağ tarafı sadeleştirelim:
    $$0{,}80 \times 7X = 5{,}6X$$

  2. Denklemi düzenleyelim:

    2X + 60 = 5{,}6X

  3. Değişkenleri bir tarafa toplayalım:

    60 = 5{,}6X - 2X = 3{,}6X

  4. X değerini bulalım:

    X = \frac{60}{3{,}6} = \frac{600}{36} = 16\frac{2}{3} \text{ litre} \; (\text{yani }16{,}666\ldots)

4. İlk Durumda A Kabındaki Su Miktarı

• A kabının ilk miktarı 2X olduğuna göre:

2X = 2 \times 16\frac{2}{3} = 33\frac{1}{3} \text{ litre}

Dolayısıyla A kabında başlangıçta 33$\tfrac{1}{3}$ litre su bulunmaktadır.

Özet Tablo

Adım İşlem Sonuç
1. Değişken Tanımı A kabı = 2 bölme = 2X, B kabı = 7 bölme = 7X A=2X,\ B=7X
2. Verilen Koşul A + 60 = \%80 \times B 2X + 60 = 0{,}80 \times 7X
3. Denklem Çözümü 2X + 60 = 5{,}6X \implies 60=3{,}6X \implies X=16\tfrac{2}{3} X=16\frac{2}{3} litre
4. Sonuç (İlk Durumda A’nın Suyu) 2X = 2\times 16\frac{2}{3} = 33\frac{1}{3} litre 33\frac{1}{3} litre

Kısa Özet

• Kapların her biri 10 eşit bölmeden oluşur. Şekle göre A kabı 2 bölme, B kabı 7 bölme doludur.
• A’ya 60 litre eklenince A’daki su, B’dekinin %80’i haline gelir.
• Değişken olarak bölme hacmine X litre dersek, 2X + 60 = 0,80 \times (7X) denklemini çözeriz.
• Sonuçta X = 16\frac{2}{3} litre bulunur ve ilk durumda A’daki su miktarı 2X = 33\frac{1}{3} litredir.

@StrawberryPuppy