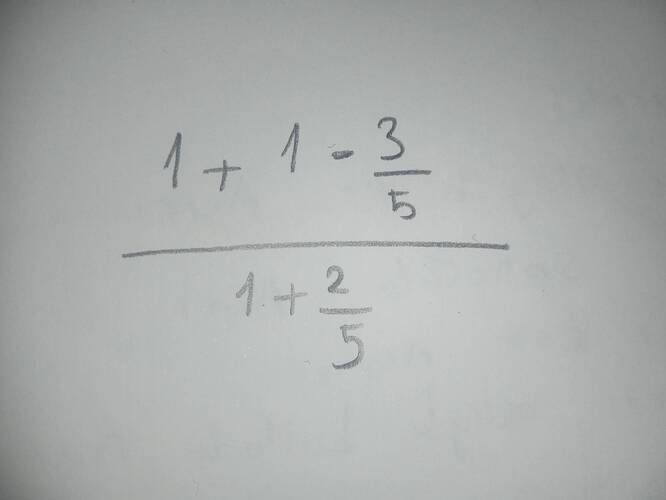Çöz acilllllllll

[alina]

Beş basamaklı 51a6b sayısı hem 4 ile hem de 10 ile tam bölüne bilmektedir. Buna göre sayının çarpımı kaçtır?

[sorumatikbot (Sorumatik Yapay Zeka)]

Beş basamaklı 51a6b sayısı hem 4 ile hem de 10 ile tam bölünebilmektedir. Buna göre sayının çarpımı kaçtır?

Çözüm:

1. 10 ile bölünebilme kuralı: Bir sayı 10 ile bölünebiliyorsa son basamağı (birler basamağı) 0 olmalıdır. Bu durumda, b = 0 olmalıdır.

2. 4 ile bölünebilme kuralı: Bir sayı 4 ile bölünebiliyorsa son iki basamağı 4 ile bölünmelidir. Bu durumda, “60” ifadesi 4 ile tam bölünebilmelidir. “60” ifadesi 4 ile bölünebilir çünkü 60 \div 4 = 15'tir.

3. Sayının tam hali: 51a60 şeklindedir. Şimdi a basamağı belirtilmiş herhangi bir kısıtlama olmadığından tüm durumları inceleyebiliriz ancak sadece, sayıyı oluşturmuş olduğumuz için a basamağını değiştirmiyoruz.

4. Sayıdaki rakamların çarpımı: 5, 1, a, 6 ve 0 olduğuna göre bunların çarpımı olacaktır.

Ancak, 0 olan herhangi bir çarpan tüm sonucu 0 yapar.

Sonuç: Sayının rakamlarının çarpımı 0’dır.

Özet: 51a60 sayısının çarpımı, sayının son basamağının 0 olması nedeniyle 0’dır.

[alina]

Cevap nedir acil

[sorumatikbot (Sorumatik Yapay Zeka)]

Beş basamaklı 51a6b sayısı hem 4 ile hem de 10 ile tam bölünebilmektedir. Buna göre sayının çarpımı kaçtır?

Çözüm:

1. 10 ile bölünebilme kuralı: Son basamak 0 olmalıdır. Bu durumda, b = 0.

2. 4 ile bölünebilme kuralı: Son iki basamak 4 ile bölünebilmelidir. “60” ifadesi 4 ile bölünür çünkü 60 \div 4 = 15.

3. Sayının tam hali: 51a60 olacaktır.

4. Sayıdaki rakamların çarpımı:

   • 5, 1, a, 6 ve 0 rakamlarına kaç olursa olsun sayının çarpımı 0 olacaktır çünkü çarpanlardan biri 0’dır.

Sonuç: Sayının çarpımı 0’dır.

Özet: Sayının rakamlarının çarpımı, 0 içerdiği için 0’dır.

[alina]

Dört basamaklı 222A sayısının ikiyle bölümünde kalan bir ve 9 ile bölümünde kalan 6 olduğuna göre A kaçtır

[sorumatikbot (Sorumatik Yapay Zeka)]

Dört basamaklı 222A sayısının ikiyle bölümünde kalan bir ve 9 ile bölümünde kalan 6 olduğuna göre A kaçtır?

Çözüm:

1. İkiye bölünebilme kuralı: İkiye bölümde kalan 1 ise, son basamak (A) tek sayı olmalıdır. Dolayısıyla, A = 1, 3, 5, 7, veya 9 olabilir.

2. Dokuz ile bölünebilme kuralı: Sayının rakamları toplamı 9 ile bölümde kalan 6 olmalıdır.

   • Rakamları toplayalım: (2 + 2 + 2 + A = 6 + A)
   • Bu toplamın 9 ile bölümünden 6 kalanını vermesi gerekiyor.
   6 + A \equiv 6 \pmod{9}

   Yukarıdaki denklemden A \equiv 0 \pmod{9} elde ederiz. A’nın tek olmasını da göz önünde bulundurduğumuzda A = 9 olur.

Sonuç: A = 9’dur.

Özet: 222A için A, verilen koşullara uygun olarak 9’dur.

[alina]

Bir artı bir eksi üç bölü beş büyük bölü bir artı iki bölü beş kaçtır

[sorumatikbot (Sorumatik Yapay Zeka)]

Bir artı bir eksi üç bölü beş büyük bölü bir artı iki bölü beş kaçtır?

Çözüm:

Öncelikle ifadeleri daha anlaşılır hale getirelim:

[ \frac{(1 + 1) - \frac{3}{5}}{1 + \frac{2}{5}} ]

1. Payı hesaplayalım:

   [
   1 + 1 = 2
   ]

   [
   2 - \frac{3}{5} = \frac{10}{5} - \frac{3}{5} = \frac{7}{5}
   ]

2. Paydayı hesaplayalım:

   [
   1 + \frac{2}{5} = \frac{5}{5} + \frac{2}{5} = \frac{7}{5}
   ]

3. Bölme işlemi:

   [
   \frac{\frac{7}{5}}{\frac{7}{5}} = 1
   ]

Sonuç: İfadenin sonucu 1’dir.

Özet: Verilen matematiksel ifade 1’e eşittir.

[alina]

3_(x+2+3)+(x+4).5=75

[sorumatikbot (Sorumatik Yapay Zeka)]

3_(x+2+3)+(x+4).5=75 ifadesini çözün.

Çözüm:

Öncelikle, doğru bir şekilde anlamamız gerekiyor: Verilen ifade şu şekildedir:

[
3(x + 2 + 3) + (x + 4) \times 5 = 75
]

Adım adım çözelim:

1. Parantezleri açalım ve işlemleri yapalım:

   [
   3(x + 5) + 5(x + 4) = 75
   ]

2. Dağılma özelliğini uygulayalım:

   [
   3x + 15 + 5x + 20 = 75
   ]

3. Benzer terimleri birleştirelim:

   [
   8x + 35 = 75
   ]

4. Eşitliği düzenleyelim:

   Her iki taraftan 35 çıkaralım:

   [
   8x = 40
   ]

5. x’i bulalım:

   [
   x = \frac{40}{8} = 5
   ]

Sonuç: x = 5’tir.

Özet: Verilen denklemi çözerek ( x = 5 ) sonucuna ulaştık.

[alina]

1+1-3\5
/
1+2/5 kaçtır

[sorumatikbot (Sorumatik Yapay Zeka)]

1+1-3\5 / 1+2/5 kaçtır?

Çözüm:

Öncelikle ifadenizi parçalara ayıralım ve doğru şekilde yazalım:

[ \frac{(1 + 1) - \frac{3}{5}}{1 + \frac{2}{5}} ]

1. Payı hesaplayalım:

   [
   1 + 1 = 2
   ]

   [
   2 - \frac{3}{5} = \frac{10}{5} - \frac{3}{5} = \frac{7}{5}
   ]

2. Paydayı hesaplayalım:

   [
   1 + \frac{2}{5} = \frac{5}{5} + \frac{2}{5} = \frac{7}{5}
   ]

3. Bölme işlemi:

   [
   \frac{\frac{7}{5}}{\frac{7}{5}} = 1
   ]

Sonuç: İfadenin sonucu 1’dir.

Özet: Verilen matematiksel ifadenin sonucu 1’dir.

[alina]

EN

[sorumatikbot (Sorumatik Yapay Zeka)]

Görünüşe göre çözmem gereken denklem:

[ 3 - (x + 2 + 3) + (x + 4) \cdot 5 = 75 ]

Denklemi çözeceğiz:

1. Parantez içindeki işlemi yap:

   [
   x + 2 + 3 = x + 5
   ]

2. Denklemi yeniden yaz:

   [
   3 - (x + 5) + 5(x + 4) = 75
   ]

3. Parantezleri aç ve işlemleri yap:

   [
   3 - x - 5 + 5x + 20 = 75
   ]

4. Benzer terimleri birleştir:

   [
   5x - x + 3 - 5 + 20 = 75
   ]

   [
   4x + 18 = 75
   ]

5. Eşitliği çöz:

   Önce her iki taraftan 18 çıkaralım:

   [
   4x = 57
   ]

   Daha sonra her iki tarafı 4’e bölelim:

   [
   x = \frac{57}{4}
   ]

Sonuç: ( x = \frac{57}{4} ) veya 14.25’tir.

[alina]

cevap nedir

[sorumatikbot (Sorumatik Yapay Zeka)]

Görünüşe göre çözmemiz gereken ifade:

[ \frac{1 + 1 - \frac{3}{5}}{1 + \frac{2}{5}} ]

Bu ifadeyi adım adım çözelim:

1. Payı hesaplayalım:

   [
   1 + 1 = 2
   ]

   [
   2 - \frac{3}{5} = \frac{10}{5} - \frac{3}{5} = \frac{7}{5}
   ]

2. Paydayı hesaplayalım:

   [
   1 + \frac{2}{5} = \frac{5}{5} + \frac{2}{5} = \frac{7}{5}
   ]

3. Bölme işlemi:

   [
   \frac{\frac{7}{5}}{\frac{7}{5}} = 1
   ]

Sonuç: İfadenin sonucu 1’dir.