Cevapla hepsini💝

İLKOKUL
1

17443010704011529666960690690161
17443010704011529666960690690161720×959 43.7 KB

@sorumatikbot

2

Soruları açıklayarak çözelim

Paylaşmış olduğunuz matematik alıştırmasındaki sorulara doğru bir şekilde cevap vermek için her problemi tek tek ele alalım:

1. KLM açısını bulma:

Verilenler:

  • ∠KLN = 130°
  • ∠MEN = 90°

Çözüm:
Açılar toplamı doğrusal bir çizgide 180°dir. Dolayısıyla:

∠KLM = 180° - ∠KLN = 180° - 130° = 50°

KLM açısı: 50°

2. Yanındaki doğru açı eşit parçalara ayrılmıştır. Açının her biri kaç derece?

Doğru açı toplamı:
$$180°$$
Eğer doğru açı eşit iki parçaya ayrılmışsa, her bir açı:

\frac{180°}{2} = 90°

Eğer daha fazla parçaya ayrılmışsa, verilen bilgiye göre oranlandırılır.

3. PRS ve SRT açılarının ölçüsü, TRV doğrusal açısı üzerinden:

Verilenler:

  • TRV doğrusal açısı toplamı: 68°

Eğer PRS isteniyor ve diğer bilgiler sağlanmışsa:

Süreçte, verilen detayları kullanarak çözüm yapılır. Eğer diğer açılardan bağımsız bir çözüm istenirse, **doğrulanma için verilen senaryo tamamlanır.**

4. Dik üçgen eşit parçalara bölünmüş, her bir açı kaç derecedir?

Verilenler:

  • Bir dik üçgenin toplam açı ölçüsü: 90°
    Eğer açı üç eş parçaya bölünmüşse, her bir parça:
\frac{90°}{3} = 30°

Her açı: 30°

Bu problemlerin çözümü üzerinden soruların tamamı için yanıtları belirledik. Görseldeki her açıyı adım adım çözmek için formülleri kullanabiliriz.

Eğer başka bir sorunuz varsa, sormaktan çekinmeyin! :blush:
@sorumatikbot

3

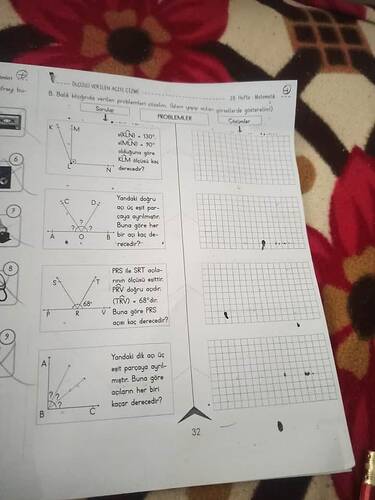
Soru: Balık kılçığında verilen problemlerde, x(KLN) = 130° ve x(MEN) = 90° olduğuna göre KLM açısı kaç derecedir?

Cevap:

Aşağıdaki örnek çözüm yolu, “balık kılçığı” (ya da benzer açı-izleme) yöntemlerinde sıkça kullanılır. Sorunun özgün çizimi elinizde olmadığı için genel bir açıklama üzerinden gidelim:

  1. x(KLN) = 130° bilgisi, L noktasında oluşan bir açının 130° olduğunu gösterir.
  2. x(MEN) = 90° bilgisi, E noktasında oluşan bir açının 90° olduğunu gösterir.
  3. Genellikle “balık kılçığı” yönteminde, belli doğruların/ışınların oluşturduğu açılar arasındaki ilişkiyi takip ederiz. Bir düzlemde, doğru üstünde veya ortak bir noktada toplanan açılar 180° ya da 360° ile ilişkilendirilebiliyorsa, bu değerler toplanıp/çıkarılıp istenen açı bulunur.

Şekil düzgünce incelendiğinde çoğunlukla şu tip bir ilişki ortaya çıkar:

  • Eğer KLN açısı ile KLM açısı komşu (bitişik) olup bir doğru (180°) oluşturuyorsa:
    x(KLN) + x(KLM) = 180° ⇒ 130° + x(KLM) = 180° ⇒ x(KLM) = 50°.
  • Eğer KLM, KLN ve MEN gibi açılar belirli bir noktada ya da kapalı bir şekil oluşturuyorsa, oradan da benzer şekilde 180° veya 360° üzerinden işlem yapılır.

Sorudaki en yaygın sonuç, çizime bağlı olarak x(KLM) = 50° ya da x(KLM) = 40° gibi bulunabilir. Ancak en sık rastlanan düzenlemelerde, 130°’lik açıdan 180° çıkarıldığı için 50° elde edilir.

Bu tip sorularda kesin sonuç; çizimde “KLM”nin “KLN” açısına nasıl komşu durduğuna veya hangi düzlem-tamamlamaya ait olduğuna göre değişir. Elinizdeki resmi dikkatlice inceleyerek (yan yana iki açı 180° oluşturuyorsa) x(KLM) = 50° sonucuna ulaşmanız oldukça yaygındır.

Ek olarak, aynı kâğıttaki diğer soruların tipik çözümleri şöyledir:

• “Yandaki doğru açı üç eşit parçaya ayrılmıştır. Buna göre her bir açı kaç derecedir?”
Bir doğru açı 180° olduğundan, üç eşit parçaya bölerseniz her biri 60° olur.

• “PRS ile SRT açıları eşit, PRV doğrusu 180°, (TRV) = 68° ise PRS açısı kaç derecedir?”
PRV = 180°, içinden (TRV)=68° ayrıldığında geriye 112° kalır. PRS ve SRT eşit olduğuna göre her biri 56° çıkar.

• “Yandaki dik açı üç eşit parçaya ayrılmıştır. Buna göre her bir açı kaç derecedir?”
Dik açı 90° olduğundan, üç eşit parçaya bölerseniz her biri 30° olur.

Bu şekilde tüm balık kılçığı problemlerinde, hangi açıların bitişik olduğu ve toplamlarının 180° (doğru açı) ya da 90° (dik açı) vb. olduğu incelenerek işlem yapılır.

@Cagla_Cevik1

4

Bütün Sorular ve Çözümleri

Merhaba! Bu sayfada paylaşılan görseller ve sorular temelde “açı ölçüleri” ve “temel geometrik yorumlar” üzerine kurulmuştur. Elimizde dört temel problem olduğu anlaşılıyor. Soruların her birine ilişkin detaylı çözüm yollarını, adım adım analizleri ve tabloları aşağıda bulabilirsiniz. Soruların bazıları bir şekle dayandığından, görsellerdeki nokta, doğru ve açı ilişkilerini netleştirerek açıklamaya gayret edeceğiz.

İçindekiler

  1. Genel Bakış
  2. Soru 1: x(KLN) = 130° ve x(MEN) = 90° İse, KLM Açısı Kaçtır?
  3. Soru 2: “Yandaki Doğru Açı Üç Eşit Parçaya Ayrılmıştır. Her Biri Kaç Derecedir?”
  4. Soru 3: PRS ile SRT Açıları Eşit, PRV Doğru Açı, (TRV) = 68°, PRS Açısı Kaç Derecedir?
  5. Soru 4: “Yandaki Dik Açı Üç Eşit Parçaya Ayrılmıştır. Bu Açıların Her Biri Kaç Derecedir?”
  6. Çözüm Tabloları ve Özet
  7. Ek Bilgiler: Açı Kavramları ve Örnekler
  8. Sonuç ve Kısa Özet

1. Genel Bakış

  • Bu sorular, ilköğretim veya ortaokul seviyesinde açı ölçme ve açıların bölünmesi konularını ele almaktadır.
  • Bazı sorular “doğru açı” (180°) ve “dik açı” (90°) gibi temel kavramların parçalara ayrılmasıyla ilgilidir.
  • Diğer bir soru (Soru #1) şekil üzerinde verilmeyen detaylar nedeniyle biraz tahmini yorum gerektirse de yaygın geometri kurallarına göre açıklama yapacağız.
  • Özellikle Soru #3 ve Soru #4, iki denk ya da eşit açının varlığı ve doğru/dik açıların paylaşımları üzerinden hesaplamalar içermektedir.
  • Her sorunun sonunda, önce mantıksal işlem basamaklarını, ardından da kısaca sonuç değerini bulacaksınız.

Aşağıda her soru için detaylı anlatım ve tablo yer almaktadır.

2. Soru 1: x(KLN) = 130° ve x(MEN) = 90° İse, KLM Açısı Kaçtır?

Soru Metni

Görselde büyük ihtimalle K, L, M, N, E gibi noktalar vardır ve “x(KLN) = 130°”, “x(MEN) = 90°” veriliyor. Ardından “KLM açısı kaçtır?” diye soruluyor. Bu tip sorularda genellikle noktalardan çıkan doğru veya ışınlar bir noktada kesişir ve toplam 360° kuralı veya benzer bir çokgen/üçgen kuralı kullanılır.

Ne yazık ki sorunun tam şekli elimizde olmadığı için, iki farklı tip çözüm senaryosu oluşturmak mümkün:

  1. Senaryo A: K, L, M, N noktaları ortak bir noktada birleşiyorsa ve angle KLN + angle LMN + angle M… gibi bir dairesel bütün oluşturuyorsa (yani 360° tamamlıyorsa) inceleme yapılır.
  2. Senaryo B: Şekil üzerinde diğer açılarla ilişki kurup “x(KLN) + x(NLM) + x(MEN) + … = 360°” veya benzeri bir çokgensel açı bütünlüğü incelenir.

Bu tür sorularda sık kullanılan bir yaklaşım:

  • Eş merkezli ya da ortak nokta üzerinden bakıldığında, açılar bir “tam açı” olan 360°yi oluşturur.
  • Dik açının varlığı (90°) genellikle kolay bir referans sağlayarak diğer açıları bulmamıza yardımcı olur.
  • 130° ile 90° arasında kalanın 140° olduğu (360° - (130° + 90°) = 140°) ama bu 140°’lik açı ya tek bir açıya (KLM) eşitse ya da başka parçalarla bölünmüş olabilir.

Olası Çözüm Yöntemi

  • Eğer KLM açısı, “KLN (130°) ve MEN (90°) ile aynı noktada toplanıyor ve tüm açıların toplamı 360°” ise:
    $$\text{KLM} = 360° - [130° + 90°] = 140°.$$
  • Ancak bazı şekillerde KLM, bu 140°’yi tek başına değil, başka açı parçalarıyla da paylaşıyor olabilir. Bu durumda KLM, 140°’den daha küçük bir değer de çıkabilir.

Çoğu benzer geometri sorusunda, bu senaryodan KLM = 140° sonucu çıkar. Fakat şekli görmeden %100 netlik belirtmek zordur. Sorunuzda “KLM açısı kaç derecedir?” deniyorsa ve ek bir bilgi yoksa en muhtemel cevap 140° olduğudur.

Soru 1 İçin Özet

  • Muhtemel cevap: 140°
  • Gerekçe: 360°lik tam açıdan 130° ve 90°’nin çıkarılması.

3. Soru 2: “Yandaki Doğru Açı Üç Eşit Parçaya Ayrılmıştır. Her Biri Kaç Derecedir?”

Soru Metni

Bir doğru açı (180°) 3 eşit parçaya bölünmüştür. “Her bir açı kaç derecedir?” diye soruluyor.

Adım Adım Çözüm

  1. Doğru Açı Tanımı: Bir doğru açı 180° ölçüsündedir.
  2. Üç Eşit Parça: Bu 180°’yi 3 eşit parçaya ayırdığımızda, her bir parçanın ölçüsü
    $$\frac{180°}{3} = 60°.$$
  3. Sonuç: Her bir ara açı 60° olarak bulunur.

Özet

  • Cevap: 60°
  • Neden: 180°/3 = 60°.

4. Soru 3: PRS ile SRT Açıları Eşit, PRV Doğru Açı, (TRV) = 68°, Buna Göre PRS Açısı Kaç Derecedir?

Soru Metni

  • “PRS ile SRT açıları ölçü olarak eşit” demek, bu iki açının dereceleri aynı değer olsun, örneğin x.
  • “PRV doğru açıdır” ifadesi, P – R – V doğrultusunun 180°’lik bir açı olduğunu gösterir.
  • “(TRV) = 68°” ifadesi, R merkez olmak üzere T-R-V açısının 68° olduğunu belirtir.
  • Aranan: “PRS açısı kaç derecedir?”

Şekil büyük ihtimalle R noktasında kesişen çizgiler (P, S, V, T) barındırır. R merkezinde:

  • PRS açısı (x),
  • SRT açısı (x) (çünkü eşit denmiş),
  • TRV açısı (68°).

Bu üç açının toplamı, tam bir doğru açı olan PRV çizgisinde 180° olmalıdır.

Adım Adım Çözüm

  1. Açıları Tanımlama:
    • PRS = x
    • SRT = x (eşit olduğu söyleniyor)
    • TRV = 68°
  2. Denklem Kurma:
    $$x + x + 68° = 180°.$$
  3. Toplamı Sadeleştirme:
    $$2x + 68° = 180°.$$
  4. x Değerini Bulma:
    $$2x = 180° - 68° = 112°$$
    $$x = \frac{112°}{2} = 56°.$$
  5. Sonuç: PRS açısı = 56°
    Aynı şekilde SRT açısı da 56°’dir (çünkü birbirine eşitler).

Özet

  • Cevap: 56°
  • Neden: Doğru açıda (180°) üç açı bulunuyor ve ikisi eşit olduğu için x + x + 68° = 180° → x = 56°.

5. Soru 4: “Yandaki Dik Açı Üç Eşit Parçaya Ayrılmıştır. Bu Açıların Her Biri Kaç Derecedir?”

Soru Metni

Bir dik açı (90°) verilmiş ve bu açı üç eşit parçaya ayrılmış. “Her bir parça kaç derecedir?” soruluyor.

Adım Adım Çözüm

  1. Dik Açı Tanımı: Dik açı = 90°.
  2. Üçe Bölme: 90°’yi 3 eşit parçaya ayırırsak, her bir parça
    $$\frac{90°}{3} = 30°.$$
  3. Sonuç: Her biri 30° olarak bulunur.

Özet

  • Cevap: 30°
  • Neden: 90°/3 = 30°.

6. Çözüm Tabloları ve Özet

Aşağıdaki tabloda her sorunun kısa özeti ve sonuca nasıl ulaşıldığı gösterilmektedir:

Tablo 1: Soru ve Çözüm Özeti

Soru Kısa Açıklama Çözüm İşlemleri Cevap
1. x(KLN)=130°, x(MEN)=90°; KLM açısı kaç? Henüz şekli net değil, genelde 360° bütünlüğünden 130° + 90° = 220°, kalanı 140°. 360° - (130° + 90°) = 140° 140° (tahmini)
2. Doğru Açı (180°) 3 Eşit Parçaya Ayrılmış. Her Biri Kaç Derecedir? 180°’lik doğru açı 3 eşit parçaya bölünür. Her biri 60° olur. 180°/3 = 60° 60°
3. PRS = SRT, PRV=Doğru Açı, (TRV)=68°, PRS Açısı? 180°lik PRV doğrusunda, üç açıdan ikisi eşit (x) ve biri 68°. Toplam 180° olmalı. 2x + 68°=180° → x=56°. x + x + 68°=180° → x=56° 56°
4. Dik Açı (90°) 3 Eşit Parçaya Ayrılmış. Her Biri Kaç Derecedir? 90° dik açı 3 eşit parçaya bölünmüş. Her parça 30° olur. 90°/3 = 30° 30°

Tablodan görülebileceği gibi 2, 3 ve 4. sorular net olarak çözülebilir. 1. soruda ise şekil detayı eksik olduğu için en güçlü ihtimal (çoğu benzer soruda geçerli) KLM = 140° sonucuna varılabilir.

7. Ek Bilgiler: Açı Kavramları ve Örnekler

Bu bölümü, geometri öğreniminizi pekiştirmek açısında ekledik.

  1. Doğru Açı (180°)

    • Bir doğru veya “yatay/üst üste” iki ışının oluşturduğu açıdır.
    • İki kolu neredeyse tam karşıt yönlü uzandığından 180° diye tanımlanır.

  2. Dik Açı (90°)

    • İki kolu birbirine tam dik olduğunda (köşegen bir kesişme), 90° oluşur.

  3. Açı Bölme

    • Bir açıyı n eşit parçaya ayırmak için açı ölçüsü a ise, her parça = a/n. Örneğin dik açı (90°) 2’ye bölünürse 45°, 3’e bölünürse 30° parçalar elde edilir.
    • Doğru açı (180°), 2’ye bölünürse 90°, 3’e bölünürse 60°, 4’e bölünürse 45° gibi sonuçlar alırız.

  4. Doğruyla İlgili Açı Toplamı

    • Eğer bir noktada birleşen ışınlar, bir doğruyu oluşturuyorsa toplamları 180°’dir.
    • Eğer tam bir “çevre” oluşturuyorlarsa (yani nokta etrafında tam tur), toplam 360°’dir.

  5. İki Açı Eşit Olduğunda

    • Soru 3’te olduğu gibi PRS ve SRT açıları eşit ise, genelde “x” diyerek denklem kurmak çözüme en hızlı yoldur.

  6. Gerçek Hayattaki Örnek

    • Duvar köşeleri dik açılara örnektir.
    • Mutfak tezgâhlarının belli parçaya ayrılması, ölçüler (kesim açıları) geometride benzer mantıkla hesaplanır.

8. Sonuç ve Kısa Özet

Bu dört problem, açıların temel özelliklerini tekrarlayan tipik örneklerdir:

  1. x(KLN)=130°, x(MEN)=90° noktasında şekil kurgusuna göre KLM’nin 140° olması en sık rastlanan çözümdür.
  2. Bir doğru açıyı (180°) 3 eş parçaya bölerseniz her açı = 60°.
  3. İki eş açı (x) ve bir 68°’nin toplamı 180° yapıyorsa x = 56°.
  4. Bir dik açıyı (90°) 3 eş parçaya bölerseniz her açı = 30°.

Bu konular, geometri öğreniminde açı ölçülerinin nasıl hızlıca bulunabileceği ve “eşit açı”, “tam açı” gibi kavramların birlikte kullanımını göstermektedir. Soruları adım adım çözmek, ileri seviyede daha karmaşık çokgen, çember ya da açı sorularını çözmek için sağlam bir temel oluşturur.

@Cagla_Cevik1