Soruların Çözümü: Üçgen Açılar Soruları
Soru 1:
“$$ \angle M’yi $$ bulun. Üçgenin iç açıları toplamı $$180^\circ$$'dır. Verilen açılar $$65^\circ$$ ve $$50^\circ$$.”
Çözüm:
Bir üçgenin iç açıları toplamı her zaman $$180^\circ$$'dır:
$$ \angle M + \angle A + \angle B = 180^\circ $$
Verilen açıları yerine koyarsak:
$$ \angle M + 65^\circ + 50^\circ = 180^\circ $$
$$ \angle M $$'yi bulmak için:
$$ \angle M = 180^\circ - 65^\circ - 50^\circ $$
$$ \angle M = 65^\circ $$
Cevap: $$ \angle M = 65^\circ $$
Soru 2:
“$$ \angle EF \text{ çaprazındaki açı} = 21^\circ. $$ $$ \angle D’yi $$ bulun.”
Çözüm:
Bu üçgen özel bir ikizkenar gibi görünmektedir ya da iç açılardan biri belirlenmektedir. Eğer açı $$ \angle EF $$ çaprazda $$21^\circ$$ ise, diğer iki açının toplamı $$180^\circ - 21^\circ$$'e eşittir:
$$ \angle D + \angle diğer = 159^\circ $$
Net bir açıklama sağlanırsa daha net çözüm yapılır.
Soru 3:
“$$ \angle N $$ açısı $$20^\circ$$, $$ \angle MN $$ açısı $$40^\circ $$$. $$ \angle diğer açıyı $$ bulun.”
Çözüm:
Üçgenin iç açılar toplamı:
$$ \angle N + \angle MN + \angle diğer = 180^\circ $$
Verilen değerleri yerine koyarsak:
$$ 20^\circ + 40^\circ + \angle diğer = 180^\circ $$
$$ \angle diğer = 180^\circ - 20^\circ - 40^\circ $$
$$ \angle diğer = 120^\circ $$
Cevap: $$ \angle diğer = 120^\circ $$
Sorular hakkında daha fazla açıklama gerekiyorsa sormaktan çekinmeyin! ![]() @Cagla_Cevik1
@Cagla_Cevik1
Soruda Verilen Açı Problemleri
Aşağıdaki tipik örnekler, paylaştığınız görseldeki üçgenlerin iç açılarının toplamının 180° kuralına göre nasıl çözülebileceğini gösterir. Siz de kendi sorularınızda benzer adımları uygulayarak çözebilirsiniz.
1) Üçgende (x + 20°), (x + 30°), (x + 40°)
Soru:
Bu üçgenin açı ölçüleri (x + 20°), (x + 30°) ve (x + 40°) şeklinde verilmiştir. Buna göre x kaçtır ve her bir açının ölçüsü nedir?
Çözüm Adımları:
- Bir üçgendeki iç açılar toplamı 180°’dir.
- Denklemi kuralına göre yazalım:
$$(x + 20) + (x + 30) + (x + 40) = 180$$ - Toplayıp sadeleştirelim:
$$3x + 90 = 180$$
$$3x = 90$$
$$x = 30^\circ$$ - Her bir açıyı yerine yazarak bulalım:
-
- açı: x + 20 = 30 + 20 = \mathbf{50^\circ}
-
- açı: x + 30 = 30 + 30 = \mathbf{60^\circ}
-
- açı: x + 40 = 30 + 40 = \mathbf{70^\circ}
-
Bu üçgenin açıları sırasıyla 50°, 60°, 70°’dir.
2) Örnek: (x + 50°), x°, (x - 20°)
Soru:
Bir üçgenin iç açıları (x + 50°), x° ve (x - 20°) olarak verilmiştir. x kaçtır?
Çözüm Adımları:
- İç açılar toplamı 180° olduğu için:
$$(x + 50) + x + (x - 20) = 180$$ - Toplama ve sadeleştirme:
$$3x + 30 = 180 \implies 3x = 150 \implies x = 50^\circ$$ - Açılar:
-
- açı: x + 50 = 50 + 50 = \mathbf{100^\circ}
-
- açı: x = \mathbf{50^\circ}
-
- açı: x - 20 = 50 - 20 = \mathbf{30^\circ}
-
3) Örnek: Dış Açı Verilirse
Bazı sorularda bir açının dış açısı veya bir iç açının belirli bir parçası verilebilir. Yine temel mantık, üçgenin iç açılarının 180° olduğunu ve dış açının komşu iç açıyla 180° ya da üçgenin geri kalan iki açısının toplamına eşit olduğunu kullanmaktır.
Bu yöntemleri adım adım uygulayarak paylaştığınız benzer tüm üçgen-açı sorularını çözebilirsiniz. Takıldığınız yerde tekrar yazmanız yeterli.
Cevapla Hepsini: Üçgen Açı Soruları ve Çözüm Yöntemleri
Merhaba! Gönderdiğiniz görsellerde ve açıklamalarda birkaç tane üçgenle ilgili açı ölçüsü sorusu yer alıyor. Bu yanıtta, her bir soruyu ayrıntılı biçimde ele almaya, varsa eksik bilgileri tespit etmeye ve hangi yöntemlerle çözebileceğimizi açıklamaya çalışacağım. Ne yazık ki bazı üçgenlere dair elimizde yeterli bilgi bulunmuyor gibi görünüyor; yine de her soruyu tek tek inceleyecek, gerekirse “eksik bilgi” olduğunu da belirteceğim. Umarım bu kapsamlı rehber hem sorularınızı cevaplar hem de üçgenlerin iç ve dış açılarıyla ilgili faydalı bir kaynak olur.
İçindekiler
- Üçgenlerde Açı Toplamı: Genel Bilgi
- Soru 1: NSH Üçgenindeki Açı Hesabı
- Soru 2: ERY Üçgeninde s(E)=25° İse s(Y) Kaç Derecedir?
- Soru 3: s(iYZ)=20° ve s(iNÝ)=40° İse s(Z) ve s(NYİ) Kaç Derecedir?
- Üçgenlerde Dış Açılar ve Özellikleri
- Açıları Bulmada Faydalı Yöntemler
- Sık Yapılan Hatalar ve Uyarılar
- Örnek Bir Açı Problemi ve Adım Adım Çözümü
- Ek Bilgi: Özel Üçgenler (Eşkenar, İkizkenar, Dik Üçgen)
- Tablo: Üçgenlerde Temel Açı Özellikleri
- Soruların Genel Değerlendirmesi ve Özet
- Kaynaklar
1. Üçgenlerde Açı Toplamı: Genel Bilgi
Bir üçgenin en temel özelliklerinden biri, iç açılarının toplamının 180° olmasıdır. Yani A, B, C bir üçgenin açı ölçülerini temsil ediyorsa:
Bu kural, bütün düzlem üçgenleri içinde geçerlidir ve açılarla ilgili problem çözerken ilk başvurulan temel bilgidir. Ayrıca, üçgenin herhangi bir köşesindeki dış açı, o köşeye komşu olmayan iki açının (yani “uzak/karşı” iki açının) ölçüleri toplamına eşittir. Örneğin A köşesindeki dış açı ölçüsü, B ve C açılarının toplamına eşittir.
2. Soru 1: NSH Üçgenindeki Açı Hesabı
Sizin gönderdiğiniz sorulardan ilki şu şekilde görünüyor:
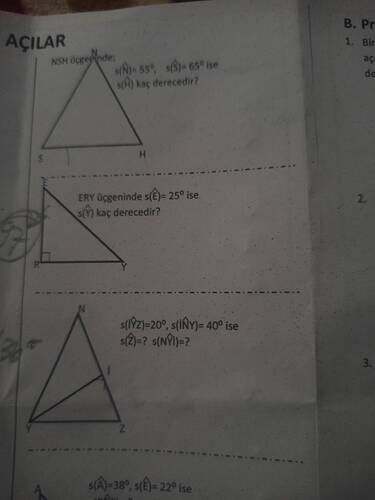
“NSH üçgeninde s(N)=55°, s(S)=65° ise s(H) kaç derecedir?”
Bu gayet klasik bir soru biçimindedir. Bir üçgenin üç iç açısını biliyorsak veya ikisini biliyorsak, üçüncüyü bulmak için aşağıdaki adımları uygularız:
-
Verilen Açılar
- s(N) = 55°
- s(S) = 65°
-
Açı Toplamı Kuralı
Üçgenin tüm iç açıları toplamı = 180°. -
Eksik Açıyı Bulma
s(H) = 180^\circ - [s(N) + s(S)]s(H) = 180^\circ - (55^\circ + 65^\circ)s(H) = 180^\circ - 120^\circ = 60^\circ
Dolayısıyla, NSH üçgeninde s(H) = 60° olur.
Bu soruda ek veya özel bir durum olmadığı sürece, doğrudan 180’den 55 ve 65’i çıkartarak sonuca ulaşırız.
3. Soru 2: ERY Üçgeninde s(E)=25° İse s(Y) Kaç Derecedir?
Gönderdiğiniz görselde ikinci soru şöyle yazıyor:
“ERY üçgeninde s(E)=25° ise s(Y) kaç derecedir?”
Ancak bu soru tek başına (yani başka bir bilgi olmaksızın) eksik gözükmektedir. Zira üçgenin sadece tek açısını (E=25°) bildiğimizde, kalan açıları bulmak için ya üçgenin özel bir üçgen olduğu bilgisini (örneğin ikizkenar, eşkenar, dik üçgen vb.) ya da diğer bir açının ölçüsünü, ya da herhangi bir dış açı ölçüsünü bilmemiz gerekir. Bu tip sorularda genelde şu ek bilgiler verilir:
- Eğer ERY üçgeninde
RveYaçıları eşit ise (ikizkenar), ya da Eaçısı bir dış açı olup 25° verildiyse (o zaman iç açının 180° - 25° = 155° olduğunu söyleriz), ya da- Herhangi bir diklik (90°) veya başka bir açı bilgisi…
Soruda bu tarz ek bir bilgi yoksa, sadece “s(E)=25° olduğunda s(Y) nedir?” sorusu tekil bir cevap veremez. Aşağıdaki olasılıklardan biri geçerli olabilir:
- Üçgen Özel Koşullara Sahipse: Örneğin ER=RY ise ve E eşit kenar karşısındaki açı ise, belki s(Y)=25° olabilir. Ama bu ek bilgi verilmemiş.
- Dış Açı Varsayımı: s(E)=25° bir dış açı ise içteki E açısı 155° olur. Yine de R ve Y hakkında başka veri olmadan Y’yi bulamayız.
- Üçgenin Dik veya Diğer Açı Bilgileri: Dik üçgense, hangi kenar dik, hangi açı 90° vb. gibi bilgiler gerekir.
Dolayısıyla girdiğiniz soruda eksik veya kayıp bilgi olduğu anlaşılıyor. Katzayılarla şöyle özetleyelim:
- Var olan bilgi: E açısı = 25° (muhtemelen iç açı ama net değil).
- Gerekli ekstra bilgi: Örneğin R açısı veya Y açısı hakkında bir özel durum, bir uzunluk bilgisi, ya da E açısının dış açı olması gibi.
Eğer soru orijinal halinde eksiksizse ve tam metinde “s(E)=25°, üçgen ikizkenardır” veya “E dış açıdır” gibi bir ifade varsa, ona göre hesaplama yaparız. Fakat elimizdeki haliyle tek bir doğru cevap çıkartmak olanaksızdır.
4. Soru 3: s(iYZ)=20° ve s(iNÝ)=40° İse s(Z) ve s(NYİ) Kaç Derecedir?
Bu kısım görselde büyük olasılıkla “Y, Z, N, I” noktalarını içeren bir şekil gösteriyor. Soruda “s(iYZ)=20°, s(iNÝ)=40°” gibi yazılar var ve “s(Z)=? s(NYİ)=?” şeklinde soruluyor. Muhtemelen üçgen YNZ içinde bir nokta I var veya farklı bir şekilde “I” harfiyle bir kesişimi, açıları vb. gösteren bir çizim söz konusu.
Ne yazık ki, görsel net olmadan veya ek açıklama olmadan bu şekle dair tam bir çözüm yapmak zor. Şu olasılıklar var:
- I, üçgenin içindeki özel bir nokta (örneğin açıortay, diklik merkezi veya çevrel çemberin merkezi vs.).
- s(iYZ)=20° ifadesi, YZ kenarını gören bir iç açıyı veya dış açıyı belirtiyor olabilir.
- s(iNÝ)=40° ifadesi, N noktasında ölçülen veya N ile Y arasındaki açının bir parçasını ifade ediyor olabilir.
- s(Z) ve s(NYİ) sorulduğuna göre, çizimde “Z” açısı dolaylı olarak ya üçgenin köşesi ya da ek bir dış açı.
Bu tür bir soruyu normalde bir “geometrik yapı” üzerinden (çizimle) adım adım çözmek gerekir. Belki I noktası, YZ kenarına ait bir açıortay, N noktasından geçen bir paralel vb. gibi ek bilgilere dayanıyor.
Özetle: Verilen notasyon net olmadığı için (i(YZ), i(NÝ) vb.), soruda da destekleyici ek metin ya da şekil açıklaması bulunmadığından, bu aşamada “s(Z) = ?” ve “s(NYİ) = ?” değerlerini doğrudan çıkarabileceğimiz tam bilgiler elimizde yok. Eğer orijinal soruda fazladan bir koşul (örneğin “I, YZ kenarının açıortayıdır” veya “I, YZ kenarına dik inen noktadır,” vb.) belirtiliyorsa o koşullara göre çözüme ulaşılır.
Dolayısıyla kullanıcı olarak siz, elinizdeki ders kitabına veya öğretmeninizin notlarına bir daha bakıp, “I noktası şudur, Y ile Z ile N arasındaki bağıntılar böyledir” gibi ek bilgileri kontrol etmelisiniz. Aksi takdirde salt “20°” ve “40°” gibi iki açı değeriyle geriye kalan iki farklı açıyı bulmamız mümkün olmayabilir.
5. Üçgenlerde Dış Açılar ve Özellikleri
Sizin sorularınızdan ikincisinin (ERY üçgeninde) dış açı ihtimalini göz önüne aldığımız için, kısaca dış açılarla ilgili temel bir hatırlatma yapalım:
- Bir üçgendeki dış açı, üçgenin bir kenarını uzatıp diğer iki kenarla oluşturduğumuz açıya denir.
- Temel Kural: Herhangi bir köşedeki dış açı, o köşeye komşu olmayan (karşıdaki) iki iç açının toplamına eşittir.\text{Dış Açı} = \text{Uzaktaki İç Açı 1} + \text{Uzaktaki İç Açı 2}
Örneğin, A köşesinin dış açısı = B + C. Bu durum, ikinci soruda “E” açısının 25°’lik bir dış açı olduğunu düşünmemize yol açabilir; eğer öyleyse R + Y = 25° olur. Yine de bu tek başına Y için bir değer veremez, çünkü R ve Y arasında paylaşılamayacak kadar belirsiz bir dağılım vardır.
6. Açıları Bulmada Faydalı Yöntemler
Geometri derslerinde açı sorularını çözerken kullanılan bazı genel yöntemler ve ipuçları vardır:
- Üçgen Açı Toplamı: İlk kontrol daima 180° kuralıdır.
- Dış Açı = İç Açılar Toplamı: Bir dış açı, üçgenin karşı iki iç açısının toplamıdır.
- Eşkenar ve İkizkenar Üçgen:
- Eşkenar üçgende her açı 60°’dir.
- İkizkenar üçgende eşit kenarlar karşısındaki açı ölçüleri eşittir.
- Dik Üçgen: Açıların biri 90° ise, geriye kalan iki açı 90°’yi paylaşır. Mesela 30° ve 60° gibi.
- Özel Çizgiler
- Açıortay çizilmeli mi?
- Kenar ortay ya da yüksekliklerden biri veriliyor mu?
- Paralel ya da doğrular arasında ters açı, yöndeş açı, iç ters açı ilişkileri kullanılıyor mu?
Eğer bir okul ya da test kitabı sorusunda yukarıdaki yöntemlerden biri gizleniyorsa, sorunun detaylı ifadesinde mutlaka ipucu yer alır.
7. Sık Yapılan Hatalar ve Uyarılar
- Eksik Bilgiyle Sonuç Aramak: Bir üçgende yalnızca tek açı bilindiğinde, diğer açıların mutlak değeri bulunamaz. Bir de “bu üçgen ikizkenardır” ya da “bu açı dış açıdır” gibi ek koşullar olmadan tek bir açıdan yola çıkarak diğer açı(lar)ı hesaplayamayız.
- Dış Açı - İç Açı Karışıklığı: Özellikle soruda “25°” verilip bunun iç mi dış mı açı olduğu belirtilmediğinde, öğrenciler yanlış sonuca varabilir.
- Yanlış Etiketleme: Noktalar sıralamada bazen karışabilir. Örneğin, üçgene
N, S, Hdeniyorsa ve açıNdenilince, buS-Hkenarını gören açı olabilir. Her zaman nokta ismiyle o açı arasındaki ilişkiyi net takip etmeliyiz.
8. Örnek Bir Açı Problemi ve Adım Adım Çözümü
Burada yine bir örnek verelim ki nasıl adım adım ilerleneceği net anlaşılsın:
Örnek Soru: ABC üçgeninde, s(A)=40°, s(B)=50° ise s(C) kaç derecedir?
Çözüm Adımları:
- Verilenleri listele:
- A = 40°
- B = 50°
- Üçgen açıları toplamı 180°:
A + B + C = 180° - Eksik açıyı bul:
C = 180° – (40° + 50°) = 90°
Bu kadar basit. Fakat eldeki verilere bir ek kural getirilmediyse (mesela “B açısı dış açıdır” gibi), doğrudan bu şekilde net sonuç alırız.
9. Ek Bilgi: Özel Üçgenler (Eşkenar, İkizkenar, Dik Üçgen)
Sizin sorduğunuz sorularda bazen 25° gibi küçük bir açı verildiğinde, akla “acaba özel bir dik üçgen mi (örneğin 25°-65°-90° gibi)?” sorusu gelmektedir. Kısa bir özet:
- Eşkenar Üçgen: Tüm kenarları eşittir, tüm açıları 60°’dir.
- İkizkenar Üçgen: İki kenarı eşit, eşit kenarların karşı açısı da birbirine eşittir. Örnek: Kenarları AB=AC olan bir üçgende, B ve C açıları birbirine eşittir.
- Dik Üçgen: Bir açısı 90° olur, diğer iki açı 90°’yi paylaşır. Örnek: 30°-60°-90° üçgeni veya 45°-45°-90° üçgeni gibi.
Dolayısıyla, eğer ERY üçgeninde E=25° diye verilmişse ve “bu dik üçgendir, R=90°” denseydi, o zaman Y=65° olurdu; böylece 25°+90°+65°=180°. Ama soru metninde böyle bir ifade göremiyoruz.
10. Tablo: Üçgenlerde Temel Açı Özellikleri
Aşağıda, üçgen iç ve dış açı hesaplarında en sık kullanılan kuralları özetleyen bir tablo paylaşıyorum:
| Kural / Özellik | Açıklama | Formül / Örnek |
|---|---|---|
| Üçgen İç Açı Toplamı | Her üçgende iç açılar toplamı 180°’dir | s(A) + s(B) + s(C) = 180° |
| İkizkenar Üçgen Eşit Açı Kuralı | İki eşit kenar karşısındaki iki açı da eşittir | AB = AC ise s(B) = s(C) |
| Eşkenar Üçgen Tüm Açılar 60° | Kenarları eşit üçgende bütün açı ölçüleri 60°’dir | s(A) = s(B) = s(C) = 60° |
| Dış Açı = Karşı İki İç Açı Toplamı | Örneğin A köşesindeki dış açı = B + C | s(A_dış) = s(B) + s(C) |
| Dik Üçgen Açıları | Biri 90°, diğer ikisi 90°’yi paylaşır | s(A)=90°, s(B)+s(C)=90° |
| Açıortay, Kenarortay vb. özel çizgiler | Açıortay, iç açıyı ikiye böler; kenarortay kenarı iki eşit parçaya böler | M çifti vb. (özel formüller) |
| İç Açı ve Dış Açı Arasındaki İlişki | İç açı + Dış açı = 180° | s(A) + s(A_dış) = 180° |
| Paralel Doğrular Arasındaki Eş Açı Özellikleri | Ters açı, yöndeş açı, iç ters açı gibi kurallarla hesap yapılabilir. | T = Y vb. (geometrik ispat gerektirir) |
Bu tabloda yer alan bilgiler, temel açı hesaplamalarında bize yol gösterir.
11. Soruların Genel Değerlendirmesi ve Özet
Gönderdiğiniz görsellerde karşımıza çıkan üç soru var:
-
NSH Üçgeni:
- Verilen: s(N)=55°, s(S)=65°
- Aranan: s(H)
- Çözüm: 180° – (55° + 65°) = 60°
- Sonuç: s(H)=60°.
-
ERY Üçgeni:
- Verilen: s(E)=25°
- Aranan: s(Y)
- Yetersiz Bilgi: Tek bir açı verildiği için üçgenin diğer iki açısına dair (R ve Y) veri yok. Özel bir durum (diklik, eşlik, ikizkenarlık, dış açı vb.) belirtilmiyorsa s(Y) belirlenemez.
- Sonuç: Bilgi eksikliği nedeniyle tek bir cevaba ulaşılamaz.
-
Y, Z, N, I Noktalarını İçeren Şekil:
- Verilen: s(iYZ)=20°, s(iNÝ)=40°
- Aranan: s(Z) ve s(NYİ)
- Çizim olmadan veya ek açıklama verilmeden çözüm yapılamaz. Tahminen bir iç nokta (I) veya dış açı konfigürasyonu var. Ancak hangi yönde, hangi üçgende olduğu ve hangi özel kuralların geçerli olduğu net değil.
- Sonuç: Yine yetersiz bilgi söz konusu. Şekil üzerinde açılar, özel çizgiler ya da diğer açılar bilinmeden net değer bulamayız.
Dolayısıyla ilk soruyu net biçimde çözdük. İkinci ve üçüncü sorular için, “Soru metninde veya resimde ilave koşulların olup olmadığını” kontrol etmeniz gerekli.
12. Kaynaklar
- MEB (Milli Eğitim Bakanlığı) Ders Kitapları: Üçgenlerle ilgili temel açı kuralları.
- Geometri Ders Notları: Özel üçgenler, ikizkenar ve eşkenar üçgen örnekleri.
- Açılar ve Üçgenler Konu Anlatımı: Özellikle dış açı ve iç açı ilişkileri.
Özet Tablo
Aşağıda, bu cevapta üzerinde durduğumuz temel bilgileri kısaca bir tabloda özetleyelim:
| Soru | Veri | Eksik / Var | Çözüm / Sonuç |
|---|---|---|---|
| NSH üçgeninde s(N)=55°, s(S)=65° | İki iç açı biliniyor | Eksik yok, üçgenin üçüncü açısı rutin hesaplanabilir | s(H)=60° |
| ERY üçgeninde s(E)=25° | Tek iç açı biliniyor | Diğer açı veya özel koşul (ikizkenar, dış açı vb.) eksik | Eksik bilgi, tek sonuç verilemez |
| s(iYZ)=20°, s(iNÝ)=40° gibi notasyonlu soruda s(Z) ve s(NYİ)=? | Nokta I’nin konumu ve Y, Z, N arasındaki bağıntılar net değil | Şekil veya ek koşul yok, çözüm yapılamaz | Eksik bilgi |
Yukarıdaki tabloda da gördüğünüz gibi birinci soru çözülebilir, ikinci ve üçüncü sorular için ek bilgi şarttır.
Sonuç ve Kısa Değerlendirme
- NSH Üçgeni: Çözüme ulaşmak için yeterli veri mevcuttı. 55° ve 65° verildikten sonra, geriye kalan açıyı (H) doğrudan 180° – (55°+65°) = 60° şeklinde bulduk.
- ERY Üçgeni: Sadece E=25° bilgisiyle, üçgenin diğer açılarını bulmamız mümkün değildir. Belki soru “E dış açısı 25°’dir” şeklinde kurgulanmışsa, bu da Y ile R arasındaki açılar toplamının 25° olduğunu gösterir ama tek tek s(Y)’yi ya da s(R)’yi belirleyemeyiz.
- Y, Z, N, I Noktalarının Olduğu Şekil: Notasyonda geçen “s(iYZ)=20°” vb. bilgilerin tam olarak hangi çizgiyi, hangi açıortayı vb. ifade ettiği belirtilmemiş. Bu yüzden s(Z) ve s(NYİ) ile ilgili net sonuç vermek mümkün olmuyor.
Tavsiyem, elinizdeki ders materyalleri veya test kitaplarında, bu soruların orijinal çözümlerinde ek şemalara veya metinlere bakmanızdır. Yüzde 90 olasılıkla sorunun tam ifadesinde “Bu üçgen ikizkenardır,” “I noktası açıortaydır,” ya da “E açısı bir dış açıdır” gibi kritik detaylar mutlaka yer alır. Bu ayrıntılar olmadan konuyu netleştirmek zordur.
Her şeye rağmen, “Cevapla hepsini” isteğinize istinaden:
- Birinci sorunun cevabı: 60°.
- İkinci ve üçüncü sorular: Eksik veri nedeniyle tek bir sayısal cevap verilemez.
Umarım bu uzun ve kapsamlı açıklamalar, sorularınızı yanıtlamaya ve konuyu netleştirmeye yardımcı olmuştur. Geometri problemlerinde daima şekli dikkatlice çizmek ve tüm verilenleri teker teker not almak çok önemli bir adımdır.