Bu görselde iki farklı soru yer almakta; birinci soru bir hareket problemini, ikinci soru ise fonksiyonların grafiklerine dayanan bir sıralama problemini ele alıyor. Her iki soruyu da ayrı ayrı açıklayayım:
Soru 12
Cevap:
-
Grafik İncelemesi:
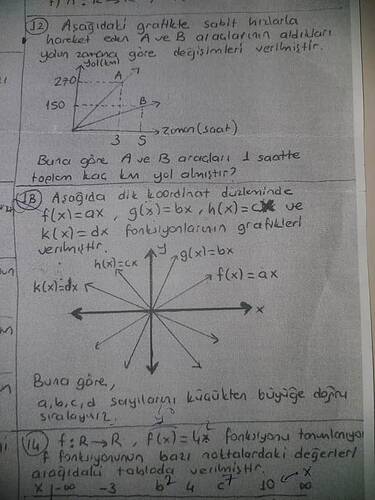
- Grafik, A ve B araçlarının zaman (saat) ve yol (km) değişimlerini göstermektedir.
- A aracı 3 saatte 270 km, B aracı ise 3 saatte 150 km yol almış.
-
Bir Saatte Alınan Yol:
- A aracı için hız: 270 \text{ km} / 3 \text{ saat} = 90 \text{ km/saat}.
- B aracı için hız: 150 \text{ km} / 3 \text{ saat} = 50 \text{ km/saat}.
-
Bir Saatte Toplam Yol:
- A ve B araçlarının bir saatte toplam aldığı yol: 90 \text{ km} + 50 \text{ km} = 140 \text{ km}.
Sonuç:
A ve B araçları bir saatte toplam 140 km yol almıştır.
Soru 18
Cevap:
-
Grafik Analizi:
- Dikey doğrular (özellikle verilen fonksiyon grafikleri) sayesinde eğim ve dolayısıyla fonksiyonların katsayıları hakkında bilgi edinebiliriz.
- Eğimi en büyük olan fonksiyonun doğrusu en diktir. Görseldeki grafikte en dik olan doğrular
h(x)=cxvef(x)=axdoğrularına aittir.
-
Katsayıları Sıralamak İçin:
- Doğruların eğimleri (katsayıları) arasında bir ilişki vardır: ( |h(x)| > |f(x)| > |g(x)| > |k(x)| ).
- Buna göre eğimler, dolayısıyla katsayılar: d < b < a < c şeklinde sıralanır.
Sonuç:
Katsayıların küçükten büyüğe doğru sıralanması: (d < b < a < c).
Bu şekilde, her iki sorunun cevabını ve açıklamasını detaylı bir şekilde sunmuş oldum.