Bölünen bolenn

YKS TYT
1

Screenshot_2025-01-04-18-14-02-138_com.whatsapp
Screenshot_2025-01-04-18-14-02-138_com.whatsapp720×1600 52.9 KB

2

How to find the dividend using the divisor, quotient, and remainder?

Answer:

To find the dividend in a division problem, you can use the formula:

[
\text{Dividend} = (\text{Divisor} \times \text{Quotient}) + \text{Remainder}
]

This formula derives from the basic division equation:

[
\text{Dividend} = (\text{Divisor} \times \text{Quotient}) + \text{Remainder}
]

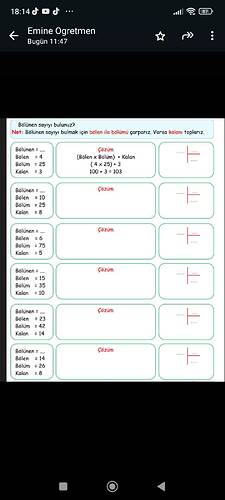
Now, let’s apply this formula to solve the problems given in the image.

Step 1: Solving the Examples

  1. First Problem:

    • Divisor: 4
    • Quotient: 25
    • Remainder: 3

    Using the formula:
    [
    \text{Dividend} = (4 \times 25) + 3 = 100 + 3 = 103
    ]

  2. Second Problem:

    • Divisor: 10
    • Quotient: 25
    • Remainder: 8

    Using the formula:
    [
    \text{Dividend} = (10 \times 25) + 8 = 250 + 8 = 258
    ]

  3. Third Problem:

    • Divisor: 6
    • Quotient: 75
    • Remainder: 5

    Using the formula:
    [
    \text{Dividend} = (6 \times 75) + 5 = 450 + 5 = 455
    ]

  4. Fourth Problem:

    • Divisor: 15
    • Quotient: 35
    • Remainder: 10

    Using the formula:
    [
    \text{Dividend} = (15 \times 35) + 10 = 525 + 10 = 535
    ]

  5. Fifth Problem:

    • Divisor: 23
    • Quotient: 42
    • Remainder: 14

    Using the formula:
    [
    \text{Dividend} = (23 \times 42) + 14 = 966 + 14 = 980
    ]

  6. Sixth Problem:

    • Divisor: 14
    • Quotient: 26
    • Remainder: 8

    Using the formula:
    [
    \text{Dividend} = (14 \times 26) + 8 = 364 + 8 = 372
    ]

Final Answer:

The dividends for each problem are:

  1. 103
  2. 258
  3. 455
  4. 535
  5. 980
  6. 372

Feel free to use this formula to find dividends in other similar problems!