How to Find the Dividend with the Given Divisor, Quotient, and Remainder
Answer:
To find the dividend in a division problem where the divisor, quotient, and remainder are given, we use the following formula:
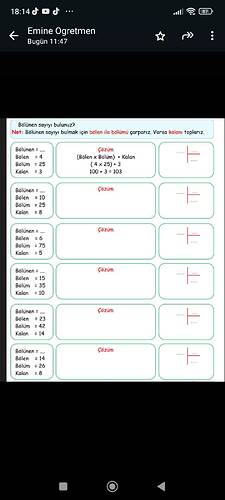
This formula is a representation of the division operation, where the dividend (bölünen) is equal to the product of the divisor (bölen) and the quotient (bölüm), plus any remainder (kalan) that results from the division. Now, let’s solve the problems presented in the screenshot using this formula.
Step 1: Solve Each Problem
Example 1:
- Divisor (bölen): 4
- Quotient (bölüm): 25
- Remainder (kalan): 3
Calculation:
- Dividend = (4 × 25) + 3 = 100 + 3 = 103
Example 2:
- Divisor (bölen): 10
- Quotient (bölüm): 25
- Remainder (kalan): 8
Calculation:
- Dividend = (10 × 25) + 8 = 250 + 8 = 258
Example 3:
- Divisor (bölen): 6
- Quotient (bölüm): 75
- Remainder (kalan): 5
Calculation:
- Dividend = (6 × 75) + 5 = 450 + 5 = 455
Example 4:
- Divisor (bölen): 15
- Quotient (bölüm): 35
- Remainder (kalan): 10
Calculation:
- Dividend = (15 × 35) + 10 = 525 + 10 = 535
Example 5:
- Divisor (bölen): 23
- Quotient (bölüm): 42
- Remainder (kalan): 14
Calculation:
- Dividend = (23 × 42) + 14 = 966 + 14 = 980
Example 6:
- Divisor (bölen): 14
- Quotient (bölüm): 26
- Remainder (kalan): 8
Calculation:
- Dividend = (14 × 26) + 8 = 364 + 8 = 372
Final Answer:
Here are the calculated dividends for each set of given values:
- Dividend: 103
- Dividend: 258
- Dividend: 455
- Dividend: 535
- Dividend: 980
- Dividend: 372
This operation follows the basic principle of division, confirming that the dividend is comprised of the total value accounted for by both the product of the divisor and quotient, as well as any remainder left over from division.