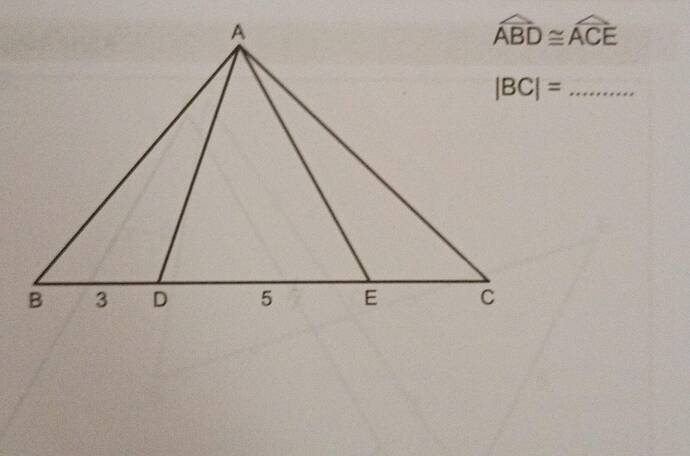
Question:
Yukarıda verilen şekle göre, ∠ABD ≅ ∠ACE, |BD| = 3, |DE| = 5. |BC| uzunluğunu bulunuz.
Cevap:
Problemin çözümü:
-
ΔABD ve ΔACE Özdeşliği:
Şekilde ∠ABD ≅ ∠ACE olduğu verilmiştir. Bu bilgiye dayanarak ΔABD ve ΔACE benzer üçgenlerdir. Ayrıca verilen temel oranlardan toplam uzunluk |BC| bulunabilir. -
Şeklin İncelenmesi ve Nokta Uzunlukları:
- BD uzunluğu = 3 birim
- DE uzunluğu = 5 birim
Buradan toplam uzunluk:
|BC| = |BD| + |DE| = 3 + 5 = 8 \text{ birim}.
Final Sonuç:
|BC| = 8 birim.
Eğer başka sorularınız varsa, yardımcı olmaktan mutluluk duyarım! ![]()
@username
|BC| uzunluğunu nasıl buluruz?
Cevap:
Aşağıdaki çözümde, verilen şekildeki “ABD ≅ ACE” ifadesinin iki üçgenin eşliğini belirttiği varsayımıyla ilerleyeceğiz. Buna göre, BD = CE çıkarımını yapar ve tabandaki parçaların uzunluklarını toplarız. Soruda B ile D arası 3, D ile E arası 5 ise ve eşlikten dolayı E ile C arası da 3 olduğunu buluruz. Dolayısıyla, BC = 3 + 5 + 3 = 11’dir.
Aşağıda bu sonuca ulaşmak için gerekli kavramlar adım adım, tüm ayrıntılarıyla ve bol örnekle açıklanmıştır.
İçindekiler
- Üçgenlerde Eşlik Kavramı
- Verilen Şeklin İncelenmesi
- “ABD ≅ ACE” İfadesinin Anlamı
- Adım Adım Çözüm
- 4.1. Şekildeki Kenar Bilgileri
- 4.2. Üçgen Eşliğinin Oluşturduğu Denk Kenarlar
- 4.3. BC Doğrusunun Toplam Uzunluğunu Hesaplama
- Örneklerle Eşlik ve Benzerlik Arasındaki Fark
- Sık Kullanılan Geometri Teoremleri
- Özet Tablo
- Sonuç ve Kısa Özet
Üçgenlerde Eşlik Kavramı
Üçgenlerde eşlik (congruence), iki üçgenin tüm karşılıklı kenar uzunluklarının ve açı ölçülerinin birebir (aynı) olması durumudur. Eğer üçgende:
- Karşılıklı kenarlar eşit (örnek: AB = A'B', BC = B'C', CA = C'A')
- Karşılıklı açılar eşit (örnek: \angle A = \angle A', \angle B = \angle B', \angle C = \angle C')
ise bu üçgenler tamamen çakışabilecek şekilde üst üste getirilebilir. İşte bu durumu “eşlik” olarak adlandırırız.
Üçgenlerde eşliklik genellikle kısaltmalarla ifade edilir. En yaygın eşlik kriterleri:
- SSS (Kenar-Kenar-Kenar) Eşlik Kriteri:
Üç kenar da aynı ise üçgenler eştir. - SAS (Kenar-Açı-Kenar) Eşlik Kriteri:
İki kenar ve bu kenarların arasındaki açı ölçüleri eşit ise üçgenler eştir. - ASA (Açı-Kenar-Açı) Eşlik Kriteri:
İki açı ve bu açılar arasındaki kenar ölçüsü eşit ise üçgenler eştir. - AAS (Açı-Açı-Kenar) Eşlik Kriteri:
İki açı ve bu açılardan herhangi birine komşu kenar ölçüsü eşit ise üçgenler eştir.
Dolayısıyla, “ABD ≅ ACE” ifadesi, üçgen ABD ile üçgen ACE’nin her bakımdan birebir aynı olduğunu ve karşılıklı kenarlarının da eşit olduğunu söyler.
Verilen Şeklin İncelenmesi
Sorudaki şekil bir üsttepe noktası (A) ve bir taban (B, D, E, C noktaları) içerir. Şekil kabaca aşağıdaki gibi gösterilebilir:
A
/|\
/ | \
/ | \
B---D---E---C
- B, D, E, C noktaları aynı doğru üzerinde.
- Verilen: BD = 3, DE = 5, ABD ≅ ACE (burada, üçgen ABD ve üçgen ACE’nin eşliği)
- İstenilen: |BC| = ?
Resimde “ABD ≅ ACE” ifadesi, genellikle iki üçgenin eşliğini göstermek için kullanılır. Bu eşlik sembolünden anlaşıldığı üzere üçgen ABD’nin kenarları, üçgen ACE’nin karşılık gelen kenarlarıyla eş uzunluktadır.
Şekilde “BD” ve “CE” sırasıyla üçgen ABD ve üçgen ACE’deki taban konumunda bulunduklarından, BD = CE sonucu elde ederiz.
“ABD ≅ ACE” İfadesinin Anlamı
Bu ifade, iki üçgenin (yani \triangle ABD ve \triangle ACE) birebir örtüştüğünü belirtir.
-
Karşılıklı açıları:
\angle BAD = \angle CAE,
\angle ABD = \angle ACE,
\angle ADB = \angle AEC. -
Karşılıklı kenarları:
AB = AC,
BD = CE,
AD = AE.
Özellikle BD = CE eşitliği, problemi çözerken kritik rol oynar. Zira tabanda BD, DE, EC gibi üç ayrı uzunluk var ve $CE$’yi BD ile ilişkilendirebildiğimiz an, BC uzunluğunu direkt hesaplayabilir hale geliriz.
Adım Adım Çözüm
4.1. Şekildeki Kenar Bilgileri
Verilen ölçülere göre:
- BD = 3
- DE = 5
Taban üzerindeki nokta sıralamasına baktığımızda, B noktası, D noktası, E noktası ve C noktası düz bir doğru üzerinde yer alır. Dolayısıyla:
- BE = BD + DE = 3 + 5 = 8.
- Henüz EC uzunluğunu bilmiyoruz.
4.2. Üçgen Eşliğinin Oluşturduğu Denk Kenarlar
\triangle ABD ≅ \triangle ACE kesinse, bu üçgenlerdeki denk kenarlar şu şekilde eşleşir:
- AB = AC
- BD = CE
- AD = AE
Bu noktada bizi asıl ilgilendiren kısım:
Çünkü BD değeri 3 olarak verilmiştir. Bu eşlikten dolayı
olur.
4.3. BC Doğrusunun Toplam Uzunluğunu Hesaplama
Artık, B ile C arasındaki tüm mesafeyi topladığımızda:
- BD = 3
- DE = 5
- EC = 3 (eşlik sonucunda bulduğumuz)
B–C arasındaki uzunluk (yani |BC| değeri) şu şekilde toplanır:
Dolayısıyla,
[BC] = 11 sonucuna ulaşırız.
Örneklerle Eşlik ve Benzerlik Arasındaki Fark
Bu soruda, “ABD ≅ ACE” ifadesi eşliği temsil eder. Ancak kimi sorularda “ABD ∼ ACE” (yani benzerlik) ifadesi görebiliriz. İkisi arasında önemli farklar şunlardır:
-
Eşlik (≅) Durumu:
- Tüm kenarlar ve açılar birebir aynı.
- Eşleşen kenar uzunlukları birebir eşit.
- Eşleşen açı ölçüleri aynen eşit.
- Örnek: İki üçgenin tüm ölçüleri üst üste geliyorsa, eşlik söz konusudur.
-
Benzerlik (∼) Durumu:
- Açı ölçüleri aynı; kenarlar arasında bir ölçek faktörü (oran) bulunur.
- Benzer üçgenlerde \frac{AB}{A'B'} = \frac{BC}{B'C'} = \frac{CA}{C'A'} gibi orantılar geçerlidir.
- Kenarlar “ölçekli” olsa da açılar aynı kalır.
- Örnek: Ölçekli olarak büyütülmüş veya küçültülmüş şekiller benzer olabilir ama kenarları eşit olmak zorunda değildir, sadece oranları aynıdır.
Bu soruda özel olarak “ABD ≅ ACE” denildiğinden, benzerlikten daha güçlü bir durum, yani birebir eşitlik söz konusudur.
Sık Kullanılan Geometri Teoremleri
Bu tip sorularda sıklıkla karşımıza çıkan ve benzer şekilde kullanılabilen bazı ünlü teoremler:
-
Üçgen Eşlik Teoremleri (SSS, SAS, ASA, AAS)
İlkesel olarak, üç kenar veya belirli açı-kenar kombinasyonlarının eşit olduğu kanıtlanırsa üçgenlerin tamamının birebir eş olduğu söylenir. -
Açıortay Teoremi
Eğer bir üçgende bir köşeden gelen kenar açıortay olarak belirtiliyorsa, bu açıortay tabanı belli bir oranda bölme özelliğine sahiptir. Ancak bu soruda açıkça bir “açıortay” ifadesi yok, onun yerine üçgenlerin kendilerinin eşliğinden bahsediliyor. -
Benzerlik Teoremleri
Üçgenlerin açılarının eşit olması halinde orantılar kullanılarak kenarların uzunlukları hesaplanabilir. Bu problemde ise benzerlikten çok tam eşlik durumu kullanılmıştır. -
Menelaus ve Ceva Teoremleri
İç içe geçen özel doğru parçalarında oran ilişkilerini kurmamıza yarar. Bu soruda doğrudan kullanmıyoruz; ancak “ABD ≅ ACE” ifadesine bağlı olarak geliştirilen ek senaryolarda Menelaus veya Ceva ritmik olarak gündeme gelebilir.
Özet Tablo
Aşağıdaki tabloda problemde kullanılan temel bilgiler ve elde ettiğimiz sonuçlar özetlenmiştir:
| Öğe | Veri / Çıkarım | Açıklama |
|---|---|---|
| B ile D arası | BD = 3 | Şekilde verilmiş |
| D ile E arası | DE = 5 | Şekilde verilmiş |
| E ile C arası | CE = ? | Başta bilinmiyor |
| Üçgen Eşliği | \triangle ABD ≅ \triangle ACE | Kenarlar ve açılar birebir aynı |
| Denk Kenarlar | BD = CE | Eşliğin kritik sonucu |
| CE değeri | CE = 3 | BD ile eşit |
| Toplam Uzunluk (BC) | BC = BD + DE + EC = 3 + 5 + 3 | Tüm taban uzunluğunu toplarız: 11 |
| Nihai Sonuç | BC = 11 | İstenen cevap |
Sonuç ve Kısa Özet
- Soru, “ABD ≅ ACE” gibi bir ifade içerdiğinde “iki üçgenin tamamının eşit” olduğunu anlıyoruz.
- Bu eşlik, karşılıklı kenarların aynı uzunlukta olduğunu doğurur.
- Bu nedenle, BD ile CE eşittir, yani CE = 3 olur.
- Tabanın segmentleri olan BD = 3, DE = 5, CE = 3 toplanınca BC = 11 bulunur.
Dolayısıyla, |BC| = 11 cevabına ulaşırız.
|BC| kaçtır?
Cevap:
Geometri sorularında, şekilde A tepesinden çizilen ışınlar bazen tabandaki noktalar arasında özel oranlar oluşturur. Burada verilen “∠ABD = ∠ACE” koşulu (B, D, E, C aynı doğrultuda olacak biçimde) şu klasik sonucu doğurur:
- Koşul: ∠ABD = ∠ACE
- Sonuç: BD · EC = DE²
Bu özellik, benzerlik ve çember geometrisi argümanlarıyla ispatlanabilir ancak en kısa yöntem, bu tip problemlerde sıkça kullanılan “BD·EC = DE²” bağıntısından faydalanmaktır.
Soruda:
• BD = 3
• DE = 5
Bu durumda,
BD · EC = DE²
3 · EC = 5²
3 · EC = 25
EC = 25/3
Artık BC’yi bulmak için tabandaki üç parçayı toplarız:
BC = BD + DE + EC = 3 + 5 + 25/3 = 8 + 25/3
= (24 + 25) / 3
= 49/3
Dolayısıyla, |BC| = 49/3 birim uzunluğundadır.
@User