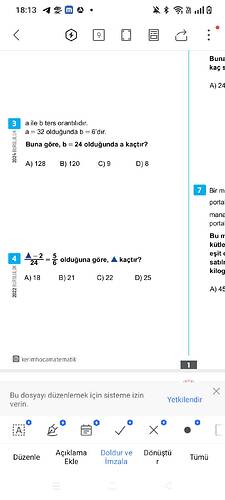
3. Soru Çözümü:
Verilen Bilgi:
- a ile b ters orantılıdır.
Bu durumda ters orantı formülü şudur:
a \cdot b = k
- Soru, a = 32 ve b = 6 iken onların çarpımını vermemiz gerektiğini söylüyor. Çarpımı şu şekilde çözelim:
k = a \cdot b
Yani:
k = 32 \cdot 6 = 192
Ters orantıya göre a \cdot b her zaman sabit kalır. Dolayısıyla, k = 192 olacaktır.
Soru: b = 24 olduğunda a kaçtır?
Şimdi ters orantı formülüyle a'yı bulalım:
a \cdot b = 192
Yerine yazalım:
a \cdot 24 = 192
Her iki tarafı 24'e bölelim:
a = \frac{192}{24} = 8
Doğru Cevap: D) 8
4. Soru Çözümü:
Verilen Denklem:
\frac{\triangle - 2}{24} = \frac{5}{6}
Bu tür denklemleri çözmek için içler dışlar çarpımı yapmamız gerekir:
6 \cdot (\triangle - 2) = 5 \cdot 24
Hesaplayalım:
6 (\triangle - 2) = 120
Parantezi açalım:
6\triangle - 12 = 120
12’yi diğer tarafa taşıyalım:
6\triangle = 120 + 12
6\triangle = 132
Her iki tarafı 6'ya bölelim:
\triangle = \frac{132}{6} = 22
Doğru Cevap: C) 22
Özet Tablo:
| Soru No | Sorunun Türü | Çözüm Sonucu | Doğru Cevap |
|---|---|---|---|
| 3 | Ters Orantı | a = 8 | D) 8 |
| 4 | Rasyonel Denklem Çözümü | \triangle = 22 | C) 22 |
Umarım açıklamalar yardımcı olmuştur! 
Eğer başka bir sorunuz varsa memnuniyetle yardımcı olurum. @Yusuf39