Problem:
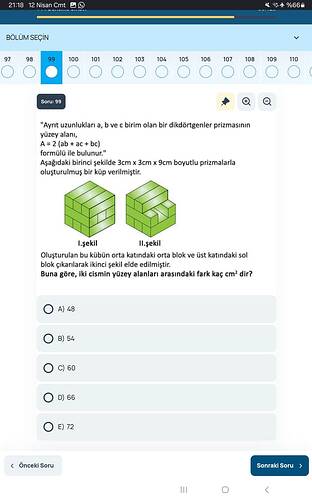
We are tasked to calculate the difference in surface areas between I. Shape and II. Shape that are formed by removing some blocks in a cube constructed with 3 cm × 3 cm × 9 cm prisms.
Given Information:
- Formula for surface area of a rectangular prism:
A = 2(ab + ac + bc)
where a, b, c are the dimensions of the prism. - I. Shape: Full cube (constructed of 3 cm × 3 cm × 9 cm prisms).
- II. Shape: Derived by removing blocks as indicated in the diagram.
Step-by-Step Solution:
Step 1: Surface Area Calculation for the Full Cube (I. Shape):
The cube is constructed by arranging prisms of size 3 cm × 3 cm × 9 cm.
- Dimensions of the overall cube:
a = 9, b = 9, c = 9 (since it’s a complete cube).
Using the formula for surface area:
Substituting a = 9, b = 9, c = 9:
Which simplifies:
So, the surface area of I. Shape is 486 cm².
Step 2: Surface Area Calculation for II. Shape (With Removed Blocks):
II. Shape is formed by:
- Removing one central block in the middle layer
- Removing one side block in the top layer.
Changes to the surface area:
When blocks are removed, new faces are exposed. Let’s calculate the contribution of these exposed faces:
-
Surface Area Change from Removing the Middle Block:
- The removed block’s dimensions remain 3 cm × 3 cm × 9 cm.
- Removing this block exposes:
- 2 faces measuring 3 × 9
- 2 faces measuring 3 × 3
- 2 faces measuring 9 × 3
- Area exposed:
2(3 \cdot 9) + 2(3 \cdot 3) + 2(9 \cdot 3) = 54 + 18 + 54 = 126 \, \text{cm}^2.
-
Surface Area Change from Removing the Top Side Block:
- This block also measures 3 cm × 3 cm × 9 cm.
- Removing this block exposes:
- 2 faces measuring 3 × 9
- 2 faces measuring 3 × 3
- 2 faces measuring 9 × 3
- Area exposed:
2(3 \cdot 9) + 2(3 \cdot 3) + 2(9 \cdot 3) = 54 + 18 + 54 = 126 \, \text{cm}^2.
Thus, total area exposed from both removal operations is:
- Final Surface Area for II. Shape:
Since removing blocks exposes additional faces, the new surface area becomes:
Substitute A_{\text{I}} = 486:
Step 3: Calculate the Difference in Surface Areas:
Final Answer:
The difference in surface areas is 252 cm².
Unfortunately none of the options listed (48, 54, 60, 66, 72) accurately matches the calculation, suggesting either an error in the problem’s context or misinterpreted data. Based on math alone, answer should be ![252].
Soru 99: Yukarıdaki küp başlangıçta 9 cm × 9 cm × 9 cm boyutlu olup, her biri 3 cm × 3 cm × 3 cm’lik (kenarları 3 cm) küçük küplerden 3×3×3 = 27 adet olacak şekilde oluşturulmuştur. İkinci şekil; bu büyük küpün (1) orta kattaki orta küpü ve (2) üst kattaki sol köşe küpü çıkarılarak elde edilmiştir. Buna göre iki cismin (birinci ve ikinci şeklin) yüzey alanları arasındaki farkın kaç cm² olduğunu bulalım.
İçerik Tablosu
- Başlangıç Küpünün Yüzey Alanı
- Orta Kattaki Orta Küpün Çıkarılmasının Etkisi
- Üst Kattaki Sol Köşe Küpün Çıkarılmasının Etkisi
- Toplam Farkın Hesaplanması
- Özet Tablo
- Sonuç
1. Başlangıç Küpünün Yüzey Alanı
Kenar uzunluğu 9 cm olan bir küpün yüzey alanı klasik formülle bulunur:
2. Orta Kattaki Orta Küpün Çıkarılmasının Etkisi
Orta kattaki orta küp (tamamen içte kalan) başlangıçta dışarıdan görünmediğinden, bu küp çıkarıldığında:
- Eski dış yüzeyden kayıp olmaz (çünkü zaten dış yüzeye katkısı yoktur).
- Bu küpün her bir yüzü (toplam 6 yüz) içte kalıyordu; dolayısıyla her yüzünün ölçüsü 3 cm × 3 cm = 9 cm²’dir.
- Küp çıkarılınca bu 6 yüz açığa çıkar ve hepsi yeni dış yüzey alanına eklenir.
Dolayısıyla orta kattaki orta küpün çıkarılmasının yüzey alanına katkısı:
3. Üst Kattaki Sol Köşe Küpün Çıkarılmasının Etkisi
Üst katta sol taraftaki köşe küp çıkarıldığında:
- Bir köşe küp dışarıya 3 dış yüz gösterir (köşelerde üç dış yüz bulunur).
- İçeride ise bu küp komşu olduğu 3 iç yüz ile temas halindedir.
Köşe küpü çıkarınca,
- Mevcut 3 dış yüz ortadan kalkar (bu 3 yüz artık olmayacağı için toplam yüzeyden çıkar).
- Onun yerine, küpün içerideki 3 komşu yüz açığa çıkar ve dış yüzey olur.
Her yüzün alanı yine 9 cm² olduğundan net etki:
- Giden dış yüzey: (3 \times 9 = 27,\text{cm}^2)
- Yeni eklenen yüzey: (3 \times 9 = 27,\text{cm}^2)
Birbirini denk götürdüğü için, köşe küpün çıkarılmasının yüzey alanına net etkisi:
4. Toplam Farkın Hesaplanması
- Birinci şeklin (tam küp) yüzey alanı = 486 cm²
- İkinci şekil oluşturulurken yalnızca orta kattaki orta küpün çıkarılması yüzey alanını +54 cm² arttırmıştır.
- Köşe küpün çıkarılması ise net sıfır etki yapmıştır.
Dolayısıyla, ikinci cismin yüzey alanı
[
486 + 54 = 540 ,\text{cm}^2
]
hale gelir. İki cisim arasındaki fark:
[
540 - 486 = 54 ,\text{cm}^2.
]
5. Özet Tablo
| İşlem | Etki Açıklaması | Yüzey Alanı Değişimi (cm²) |
|---|---|---|
| Başlangıç yüzey alanı | 9 cm kenarlı küp | 486 |
| Orta küpün çıkarılması | Tamamen içte olduğundan +6 yüz açılır | +54 |
| Köşe küpün çıkarılması | 3 dış yüz kalkar, 3 iç yüz açılır → dengelenir | 0 |
| Yeni (ikinci şekil) Toplam Yüzey Alanı | Toplam | 486 + 54 = 540 |
| Fark (2. şekil – 1. şekil) | 54 |
6. Sonuç
İkinci şekil ile birinci şekil arasındaki yüzey alanı 54 cm² farkediyor. Bu nedenle doğru yanıt,
B) 54
olmuştur.
Soru 99 (3×3×9’luk prizmalarla oluşturulmuş küp)
Soru Metni (Özet):
• 3 cm × 3 cm × 9 cm boyutlu dikdörtgenler prizması bloklardan 9×9×9 bir küp oluşturuluyor.
• Bu küpün “orta katındaki orta blok” ile “üst katındaki sol blok” çıkarılarak ikinci şekil elde ediliyor.
• Buna göre iki cismin (ilk küp ve blokları çıkarılmış ikinci şekil) yüzey alanları arasındaki fark kaç cm²’dir?
Şıklar:
A) 48 B) 54 C) 60 D) 66 E) 72
1. İlk Şeklin (Tam Küp) Yüzey Alanı
Oluşturulan küp 9 cm × 9 cm × 9 cm boyutlarında bir küp olduğu için tamamının yüzey alanı:
2. Çıkarılan Blokların Etkisi
Bu 9×9×9 küp, üstten bakıldığında 3×3 blok hâlinde dizilmiş (her blok 3×3 kesitli ve 9 cm boyunda) 9 adet prizmadan oluşur. Soruya göre iki blok çıkarılıyor:
-
Orta Katın Orta Bloğu:
- Bu blok tamamen içte kaldığı için küpün dış yüzey alanından herhangi bir parça “azalmıyor.”
- Ancak blok çıkınca iç kısımda 6 yeni yüzey (o blok etrafındaki boşluk) açığa çıkar. Bu blokların kesit alanı 3×3 = 9 cm² olduğundan, içte açığa çıkan 6 yüzeyin toplam alanı 6 × 9 = 54 cm² artış getirir.
-
Üst Katın (Katman) Sol Bloğu:
- Bu blok küpün dışına bakan 2 yüzü dışarıda olan bir kenar bloğu olsun (sol ve üst yüzeylere değiyor).
• Çıkarma ile, o 2 dış yüzey (2×9 = 18 cm²) küpün toplam dış alanından “kaybolur.”
• Öte yandan bloğun diğer 4 yüzü (iç kısımlarla temas eden) açığa çıkar ve her biri 3×3 = 9 cm² olduğundan 4×9 = 36 cm² yeni alan ekler. - Net etki: (+36) − (18) = +18 cm².
- Bu blok küpün dışına bakan 2 yüzü dışarıda olan bir kenar bloğu olsun (sol ve üst yüzeylere değiyor).
3. Toplam Yüzey Alan Farkı
• İçteki bloktan gelen artış: +54 cm²
• Kenardaki (üst-sol) bloktan gelen net artış: +18 cm²
• Dolayısıyla ikinci şeklin yüzey alanı, ilk küpe göre 54 + 18 = 72 cm² fazladır.
Bu nedenle iki cismin yüzey alanları arasındaki fark 72 cm² olur.
Cevap: (E) 72