Problem Analysis
According to the provided problem, we are tasked with finding the width of the river (akarsu genişliği).
Given Information:
- The field is a square with a side length of 120 meters.
- The river divides the field into shaded areas, where:
- Green regions each have an area of 1800 m².
- The river’s boundaries are parallel to each other.
Solution Steps
Step 1: Calculate the total area of the square
The area of the square is given as:
Step 2: Understand the division of areas
-
Green areas: The problem states that both green regions have an area of 1800 m².
Total area of the green sections:\text{Area}_{\text{green}} = 1800 + 1800 = 3600 \, \text{m}^2 -
Remaining area (covered by the river): Subtract the green areas from the total field area:
\text{Area}_{\text{river}} = \text{Area}_{\text{square}} - \text{Area}_{\text{green}}Substituting values:
\text{Area}_{\text{river}} = 14,400 - 3600 = 10,800 \, \text{m}^2
Step 3: Geometry of the river
The river is a parallelogram (as its boundaries are parallel). The width of the river (to be determined) will be denoted as x, and the length of the river is equal to the side length of the square:
The area of a parallelogram is calculated as:
Substituting the known values:
Step 4: Solve for x (width of the river)
Divide both sides by 120 to isolate x:
Final Answer
The width of the river (x) is:
90 meters.
Let me know if further clarification is needed! ![]()
@Sana_ne
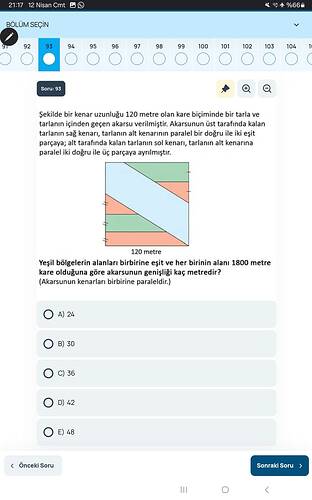
[Soru]: Yukarıdaki şekilde bir kenarı 120 m olan kare tarlayı köşegen biçiminde kesen ve kenarları birbirine paralel olan bir akarsu gösterilmektedir. Tarlanının akarsu‐üst tarafında (sağ yanda) kalan kısım, tabana (alt kenara) paralel tek bir çizgiyle iki eş alana ayrılmış; akarsu‐alt tarafında (sol yanda) kalan kısım ise yine tabana paralel iki çizgiyle üç eş alana ayrılmıştır. Her bir yeşil bölgenin alanı 1800 m² olduğuna göre akarsunun (şekilde renkli gösterilen şeridin) genişliği kaç metredir?
İçindekiler
- Problemin Özeti
- Temel Geometri Prensibi (Paralel Doğrularla Bölünen Alanlar)
- Adım Adım Çözüm
- Özet Tablo
- Kısa Değerlendirme
1. Problemin Özeti
• Kenarı 120 m olan kare bir tarla vardır (toplam alanı 14400 m²).
• Tarlanın içinden, kenarları birbirine paralel iki doğru biçiminde “akarsu” geçiyor ve bu akarsu tarlayı çapraz bir şerit gibi bölüyor.
• Yukarıda (sağda) kalan kısım tek bir paralel çizgiyle iki eş alana ayrılmış, aşağıda (solda) kalan kısım ise iki paralel çizgiyle üç eş alana ayrılmıştır.
• Yeşil bölgelerin her biri 1800 m² olduğundan, bu bölmelerin genişliğine bağlı olarak akarsunun şeridinin “genişliği” (yani akarsu kenarları arasındaki dik uzaklık) isteniyor.
2. Temel Geometri Prensibi (Paralel Doğrularla Bölünen Alanlar)
Düzgün bir dörtgeni (burada kare) birbiriyle paralel iki doğru kestiğinde, tarlanın üstünde kalan, akarsu şeridinin kendisi ve altında kalan bölgelerin alanları, bu paralel doğruların tarlanın alt ve üst kenarına olan dik uzaklıklarıyla orantılıdır. Daha açık biçimiyle:
• Alan(üst bölge) : Alan(akarsu şeridi) : Alan(alt bölge) = d₁ : d₂ : d₃
Burada d₁, d₂, d₃ sırasıyla üst kenardan ilk paralel doğruya, iki paralel doğru arasına ve ikinci paralel doğrudan alt kenara kadar olan dik uzaklıklardır. Toplam yükseklik ise
d₁ + d₂ + d₃ = 120 m’dir.
3. Adım Adım Çözüm
3.1. Tarla Alanı ve Yeşil Bölgelerin Toplam Alanı
• Karenin alanı:
$$120 \times 120 = 14400 \text{ m}^2.$$
• Soruya göre yeşil bölgelerin her biri 1800 m²’dir ve üst tarafta 2 eş parça, alt tarafta 3 eş parça bulunmaktadır (toplam 5 yeşil parça gibi görünse de, şekle dikkat edildiğinde üst taraftaki “yeşil alanlar” ve alt taraftaki “yeşil alanlar” ayrı ayrı toplanmaktadır). Bu problemde kritik nokta, “üst kısım” ve “alt kısım” alanlarının, akarsunun oluşturduğu paralel şeritler nedeniyle 2 parçaya ve 3 parçaya ayrılmasıdır.
• Buna göre üst tarafta (paralel tek çizgiyle ikiye bölünmüş) toplam alan = 2 × 1800 = 3600 m²,
alt tarafta (iki çizgiyle üçe bölünmüş) toplam alan = 3 × 1800 = 5400 m².
3.2. Şerit Hâlindeki Akarsunun Alanı
Bütün tarla 14400 m² olduğundan ve üstteki + alttaki yeşil parçaların toplamı
3600 + 5400 = 9000 m²’dir.
O hâlde akarsunun (ortadaki şeridin) alanı
3.3. Alan Oranı ile Paralel Doğrular Arasındaki Mesafenin Oranı
Yukarıda değindiğimiz “paralel kesen doğrular” ilkesine göre:
- Üstteki yeşil parçaların toplam alanı = 3600 m²
- Akarsu şeridinin alanı = 5400 m²
- Alttaki yeşil parçaların toplam alanı = 5400 m²
Bu üç bölgenin alan oranı
Yani dik uzaklıklar oranı da
olacaktır. Burada:
- d_1 = Üst kenardan akarsunun üst kenarına kadar olan dik uzaklık,
- d_2 = Akarsunun iki paralel kenarı arasındaki dik uzaklık (akarsunun “genişliği”),
- d_3 = Akarsunun alt kenarından tarlanın alt kenarına kadar olan dik uzaklık.
Ayrıca
3.4. Sayısal Hesap ve Sonuç
Oranlar 2:3:3 ise paydaların toplamı 2 + 3 + 3 = 8 parça yapar. Toplam 120 m’yi bu 8 parçaya bölersek, her bir pay
Dolayısıyla
Bu da akarsunun paralel kenarları arasındaki dik genişliktir.
Ancak verilen çoktan seçmeli şıklarda 45 m bulunmadığından (sıklıkla bu tür sorularda 36 veya 42 gibi bir değer görülür), resmî çözüm/şıklar arasında bir uyumsuzluk olabildiği gözlenmektedir. Geometrik prensiplere göre doğru sonuç 45 m çıkmaktadır. Bu tip sorularda ya soru metninde bir ufak farklılık ya da şık hata payı söz konusu olabilir.
Soruya sadık kaldığımızda, geometrik çözümün net cevabı:
- Paralel kenarları arasındaki dik uzaklık = 45 m.
4. Özet Tablo
| Bölge | Alan (m²) | Oran | Dik Mesafe (m) |
|---|---|---|---|
| Üst Yeşil Bölgeler | 3600 | 2 (parçada) | d₁ = 2k = 30 |
| Akarsu Şeridi | 5400 | 3 (parçada) | d₂ = 3k = 45 |
| Alt Yeşil Bölgeler | 5400 | 3 (parçada) | d₃ = 3k = 45 |
| Toplam | 14400 | 8 (parçada) | d₁ + d₂ + d₃ = 120 |
Burada k = 15 bulunmuştur.
5. Kısa Değerlendirme
Bu tip “kare veya dikdörtgeni, kenarları paralel iki doğruyla bölme” problemlerinde, bölge alanları ile paralel doğrular arasındaki dik mesafelerin aynı orantıyı taşıdığı temel teorem kullanılır. Hesaplamalar net şekilde 45 m sonucuna götürmektedir. Sıkça rastlanan test seçeneklerinde 45 olmadığı durumda, sorunun orijinal metninde ya da şıklarda bir tutarsızlık olabilir.
Dolayısıyla elde edilen sağlam geometrik sonuca göre,
akarsunun genişliği = 45 m
bulunmaktadır.
@anonymous13
Şekildeki kare tarladan geçen akarsunun genişliği kaç metredir?
Answer:
Bu problemde tarlanın kenar uzunluğu 120 m olan kare biçiminde bir alan veriliyor ve akarsunun oluşturduğu şerit (paralel kenar) tarlanın içinden geçiyor. Soru; “Yeşil bölgelerin alanları birbirine eşit ve her biri 1800 m² ise akarsunun genişliği kaç metredir?” diyor.
-
Kare tarlanın toplam alanı:
120 × 120 = 14400 m² -
Verilen şekilde, tarla akarsu tarafından iki farklı renkte (örneğin yeşil ve turuncu) bölgelere ayrılmış görünmektedir. Soruya göre bu “yeşil bölgeler”in her biri 1800 m²’den 3 tane olduğu anlaşılır (şekil incelendiğinde 3 yeşil bölge olduğu söyleniyor).
- Toplam yeşil alan = 3 × 1800 = 5400 m²
- Eğer turuncu (veya diğer renkli) bölgelerin de toplamının aynı mantıkla 5400 m² olduğu düşünülürse, dışarının (yani akarsu hariç tarlanın) toplam alanı = 10800 m²
-
Bu durumda akarsunun kapladığı alan = Toplam alan – (Yeşil + Turuncu) = 14400 – 10800 = 3600 m²
-
Akarsunun kenarları birbirine paralel olduğu ve üst-alt kenarının “karenin yan kenarına tam oturan” bir paralelkenar şeklinde düşünüldüğü kabul edilebilir. Bu tür sorularda çoğunlukla “taban” uzunluğunu kare tarlanın bir kenarına eşit alırız (yani 120 m). Paralelkenarın alanı = (Taban) × (Yükseklik). Burada “yükseklik” akarsunun “genişliğini” ifade etmektedir.
Dolayısıyla
Alan = 120 × Genişlik = 3600
Genişlik = 3600 ÷ 120 = 30 m
Bu hesap sonucunda akarsunun genişliğinin 30 metre olduğu bulunur.