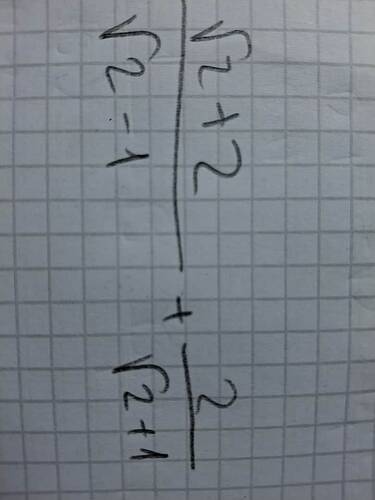Bu ifade iki ayrı kesirden oluşuyor. İfadenin tamamını sadeleştirmek ve eşleniğini almak için adım adım gidebiliriz.
İfadenin Eşleniği
-
İlk Kesir: \frac{\sqrt{2} + 2}{\sqrt{2} - 1}
Bu kesirin paydasını kökten kurtarmak için eşleniği ile çarpılır:
- Eşleniği: \sqrt{2} + 1
- Çarpım: \left(\frac{\sqrt{2} + 2}{\sqrt{2} - 1}\right) \times \left(\frac{\sqrt{2} + 1}{\sqrt{2} + 1}\right)
-
İkinci Kesir: \frac{2}{\sqrt{2} + 1}
Bu kesirin paydasını kökten kurtarmak için eşleniği ile çarpılır:
- Eşleniği: \sqrt{2} - 1
- Çarpım: \left(\frac{2}{\sqrt{2} + 1}\right) \times \left(\frac{\sqrt{2} - 1}{\sqrt{2} - 1}\right)
Sadeleştirme ve Toplama
Her iki kesir için yukarıdaki işlemleri yaparak paydaları saf hale getirip toplama işlemi yapabiliriz. Sonuç olarak birleşik bir kesir elde edilir.
Örnek:
-
İlk kesir: (\sqrt{2} + 2)(\sqrt{2} + 1) = 2 + \sqrt{2} + 2\sqrt{2} + 2 = \sqrt{2} + 4 + 2\sqrt{2}
-
İkinci kesir: 2(\sqrt{2} - 1) = 2\sqrt{2} - 2
Bu şekilde devam ederek son ifadeyi bulabiliriz. Dikkatlice işlem yaparak pay ve paydadaki sadeleştirmeleri yapmalısınız.
Özet: Yukarıdaki adımlarla köklü ifadelerin sadeleştirme ve eşleniklerini bulmak daha kolay hale gelir. Bu adımları dikkatlice uygulayarak doğru sonuca ulaşabilirsiniz.