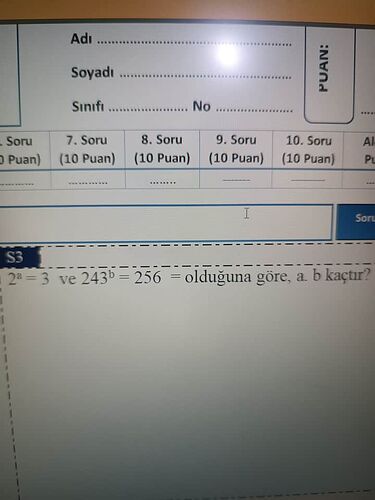
Verilen ifadelere göre, a ve b kaçtır?
Cevap:
Verilen ifadeler:
- 2^a = 3
- 243^b = 256
Bu ifadeleri çözelim.
1. İfade: 2^a = 3
Bu durumda her iki tarafın logaritmasını alabiliriz:
a \cdot \log(2) = \log(3)
Buradan a'yı bulmak için:
a = \frac{\log(3)}{\log(2)}
2. İfade: 243^b = 256
Önce tabanları asal çarpanlarına ayıralım:
- 243 = 3^5
- 256 = 2^8
Bu durumda denklem:
(3^5)^b = 2^8
Bu, aşağıdaki hale gelir:
3^{5b} = 2^8
Her iki tarafın logaritmasını alalım:
5b \cdot \log(3) = 8 \cdot \log(2)
Buradan b'yi bulmak için:
b = \frac{8 \cdot \log(2)}{5 \cdot \log(3)}
Bu sonuçları daha doğru hesaplamak için hesap makinesi kullanabilirsiniz. Ama genel süreç bu şekildedir.
Özet: a ve b yukarıdaki logaritmik ifadelerin sonucuna göre bulunur.