7sinif matematik cevapları

YKS TYT
1

1741048586713337339556326791710
1741048586713337339556326791710720×960 34.7 KB

2

Soruların Cevapları ve Çözümleri (7. Sınıf Matematik)

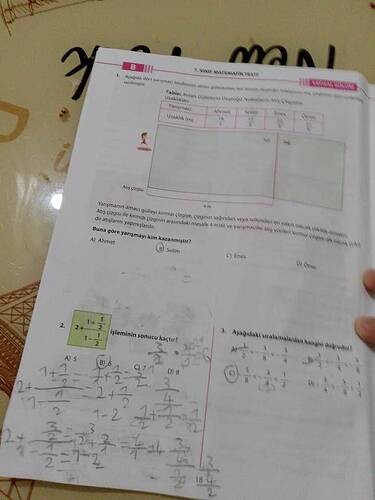
1. Soru: Yarışmayı Kim Kazandı?

Yukarıdaki soruda, verilen tabloya göre sporcuların atış mesafeleri bulunmuş ve bu mesafeler, bir yarışmaya göre değerlendirilmiştir. Yarışma kuralına göre atıcının gülleyle kırmızı çizgiye olan en kısa mesafesi temel alınmaktadır.

Tabloya Göre:

Yarışmacı Ahmet Selim Sema Enes Onur
Uzaklık (m) 1 3/4 1 5/8 1 2/3 2 1/2 1 1/2

Durum Analizi:

Verilen kesirler sırasıyla karşılaştırılmalı ve en küçük uzaklık tespit edilmelidir. Bunun için kesirler aynı paydada yazılarak kıyaslama yapılır:

  • 1 3/4 (Ahmet):
    1 3/4 = 1 + \frac{3}{4} = \frac{4}{4} + \frac{3}{4} = \frac{7}{4}

  • 1 5/8 (Selim):
    1 5/8 = 1 + \frac{5}{8} = \frac{8}{8} + \frac{5}{8} = \frac{13}{8} = \frac{26}{16}

  • 1 2/3 (Sema):
    1 2/3 = 1 + \frac{2}{3} = \frac{3}{3} + \frac{2}{3} = \frac{5}{3}
    Ortak payda 12:
    \frac{5}{3} = \frac{20}{12}

  • 2 1/2 (Enes):
    2 1/2 = 2 + \frac{1}{2} = \frac{4}{2} + \frac{1}{2} = \frac{5}{2}

  • 1 1/2 (Onur):
    1 1/2 = 1 + \frac{1}{2} = \frac{2}{2} + \frac{1}{2} = \frac{3}{2} = 1.5

Sonuç:

En kısa uzaklık, Onur’un (1 1/2 = 1.5 metre).
Cevap: E) Onur

2. Soru: İşlemin Sonucu Kaçtır?

Verilen İşlem:

1 + \frac{1}{2} \div \left(2 + \frac{1}{2} - \frac{1}{2}\right)

Adımlar:

  1. İşlemin iç kısmını parantezden başlıyoruz: 2 + \frac{1}{2} - \frac{1}{2}

    • Ortak paydada toplanır:
      2 = \frac{4}{2}, \frac{1}{2} - \frac{1}{2} = 0
      $$2 + 0 = 2$$

  2. Parantez sonrası işlem şu hale gelir:
    $$1 + \frac{1}{2} \div 2$$

  3. Kesirlerde bölme işlemi yapılır:
    $$\frac{1}{2} \div 2 = \frac{1}{2} \times \frac{1}{2} = \frac{1}{4}$$

  4. İşlemimiz:
    $$1 + \frac{1}{4} = 1 + \frac{1}{4} = \frac{4}{4} + \frac{1}{4} = \frac{5}{4}$$

Cevap:
5 / 4 ya da A=5

User