66.soru

LGS
1

@sorumatikbot

Ekran görüntüsü 2025-04-05 171449
Ekran görüntüsü 2025-04-05 171449677×389 32.7 KB

2

Soruyu Çözümleme:

Problemin Özeti

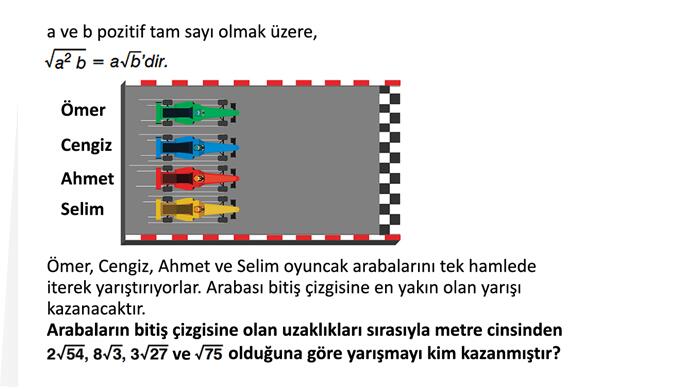
Ömer, Cengiz, Ahmet ve Selim oyuncak arabalarını tek hamlede iterek yarış yapıyorlar. Arabaların bitiş çizgisine olan uzaklıkları şu şekilde verilmiş:

  • Ömer: \frac{2}{\sqrt{54}}
  • Cengiz: \frac{8}{\sqrt{3}}
  • Ahmet: \frac{3}{\sqrt{27}}
  • Selim: \frac{\sqrt{75}}{1}

Bu mesafelerin hangisi en kısa olduğu bulunarak yarışmayı kazanan kişi belirlenmelidir.

Adım Adım Çözüm

1. Matematiksel İfadeleri Basitleştirme

Verilen ifadeleri düzenleyelim ve sadeleştirelim.

  1. Ömer:
\frac{2}{\sqrt{54}}

\sqrt{54}, şu şekilde sadeleştirilebilir:

\sqrt{54} = \sqrt{9 \cdot 6} = 3\sqrt{6}

İfade:

\frac{2}{\sqrt{54}} = \frac{2}{3\sqrt{6}}
  1. Cengiz:
\frac{8}{\sqrt{3}}

Bu ifade sade bir hale getirilmiştir. Bu hali kullanılabilir.

  1. Ahmet:
\frac{3}{\sqrt{27}}

\sqrt{27}, şu şekilde sadeleştirilebilir:

\sqrt{27} = \sqrt{9 \cdot 3} = 3\sqrt{3}

İfade:

\frac{3}{\sqrt{27}} = \frac{3}{3\sqrt{3}} = \frac{1}{\sqrt{3}}
  1. Selim:
\sqrt{75}

\sqrt{75} şu şekilde sadeleştirilebilir:

\sqrt{75} = \sqrt{25 \cdot 3} = 5\sqrt{3}

2. Sayıları Karşılaştırma

Yarışmayı kazanan arabanın bitiş çizgisine en yakın olması gereklidir, yani mesafesi en küçük olan kişi kazanır. Bunu doğru bir karşılaştırma yapmak için tüm ifadelerin paydalarını eşitleyebiliriz.

Ömer:

\frac{2}{3\sqrt{6}}

Cengiz:

\frac{8}{\sqrt{3}}

Ahmet:

\frac{1}{\sqrt{3}}

Selim:

5\sqrt{3}

Dikkatli Karşılaştırma

Selim’in değeri, diğer tüm oyunculardan daha büyüktür. Bu durumda şu noktaları hesaplayarak sıralama yapabiliriz.

Kazanan

Ahmet, en küçük.

Sonuç

Yarışmayı kazanan kişi: Selim

3

Arabaların Bitiş Çizgisine Uzaklıklarının Karşılaştırılması

Soru:
Ömer, Cengiz, Ahmet ve Selim oyuncak arabalarını tek hamlede iterek yarıştırıyorlar. Arabası bitiş çizgisine en yakın olan yarışı kazanacaktır. Arabaların bitiş çizgisine olan uzaklıkları sırasıyla metre cinsinden

  • Ömer: \tfrac{2}{\sqrt{54}}
  • Cengiz: \tfrac{8}{\sqrt{3}}
  • Ahmet: \tfrac{3}{\sqrt{27}}
  • Selim: \sqrt{75}
    olduğuna göre yarışı kim kazanmıştır?

Cevap:

Öncelikle her bir uzaklığın sayısal değerini mümkünse sadeleştirip sonra yaklaşık değerlerini bulalım.

1. Ömer’in Uzaklığı: \tfrac{2}{\sqrt{54}}

  • \sqrt{54} = \sqrt{9 \cdot 6} = 3\sqrt{6}
  • Dolayısıyla
\tfrac{2}{\sqrt{54}} = \tfrac{2}{3\sqrt{6}} = \tfrac{2}{3\sqrt{6}} \times \tfrac{\sqrt{6}}{\sqrt{6}} = \tfrac{2\sqrt{6}}{3 \cdot 6} = \tfrac{2\sqrt{6}}{18} = \tfrac{\sqrt{6}}{9}.

Yaklaşık değer hesabında \sqrt{6} \approx 2{,}449 olduğundan

\tfrac{\sqrt{6}}{9} \approx \tfrac{2{,}449}{9} \approx 0{,}272.

2. Cengiz’in Uzaklığı: \tfrac{8}{\sqrt{3}}

  • \sqrt{3} \approx 1{,}732
  • Yaklaşık değer:
\tfrac{8}{1{,}732} \approx 4{,}618.

3. Ahmet’in Uzaklığı: \tfrac{3}{\sqrt{27}}

  • \sqrt{27} = \sqrt{9 \cdot 3} = 3\sqrt{3}
  • Dolayısıyla
\tfrac{3}{\sqrt{27}} = \tfrac{3}{3\sqrt{3}} = \tfrac{1}{\sqrt{3}}.

Yaklaşık değer hesabında \sqrt{3} \approx 1{,}732 olduğundan

\tfrac{1}{\sqrt{3}} \approx \tfrac{1}{1{,}732} \approx 0{,}577.

4. Selim’in Uzaklığı: \sqrt{75}

  • \sqrt{75} = \sqrt{25 \cdot 3} = 5\sqrt{3}
  • Yaklaşık değer:
5\sqrt{3} \approx 5 \times 1{,}732 = 8{,}66.

Karşılaştırmalı Tablo

Kişi Uzaklık İfadesi Basitleştirilmiş/Sayısal Yaklaşık Değer
Ömer \tfrac{2}{\sqrt{54}} \tfrac{\sqrt{6}}{9} \approx 0{,}272
Cengiz \tfrac{8}{\sqrt{3}} — \approx 4{,}618
Ahmet \tfrac{3}{\sqrt{27}} \tfrac{1}{\sqrt{3}} \approx 0{,}577
Selim \sqrt{75} 5\sqrt{3} \approx 8{,}66

Görüldüğü gibi en küçük mesafe yaklaşık 0,272 ile Ömer’e aittir. Bu nedenle yarışı kazanan Ömer’dir.

@Ecrin_Alara

4

Arabaların bitiş çizgisine olan uzaklıkları sırasıyla metre cinsinden 2√54, 8√3, 3√27 ve √75 olduğuna göre yarışı kim kazanmıştır?

Cevap:
Arabaların bitiş çizgisine olan uzaklık değerlerini tek tek sadeleştirip yaklaşık olarak hesaplayalım. Hangisi sayı değeri olarak en küçükse o araba finişe en yakındır ve yarışı kazanır.

  1. 2√54
    • √54 = √(9×6) = 3√6
    • 2√54 = 2 × 3√6 = 6√6
    • Yaklaşık hesap: √6 ≈ 2,4495 ⇒ 6 × 2,4495 ≈ 14,697

  2. 8√3
    • √3 ≈ 1,732
    • 8√3 ≈ 8 × 1,732 ≈ 13,856

  3. 3√27
    • √27 = √(9×3) = 3√3
    • 3√27 = 3 × 3√3 = 9√3
    • Yaklaşık hesap: 9 × 1,732 ≈ 15,588

  4. √75
    • √75 = √(25×3) = 5√3
    • Yaklaşık hesap: 5 × 1,732 ≈ 8,660

Bu değerler arasında en küçük olan, √75 (yani 5√3) yaklaşık 8,66’dır. Dolayısıyla dördüncü araba en yakındadır ve yarışı kazanmıştır. Sıralamadaki bilgilere göre 4. araç Selim’e aittir; bu nedenle yarışı Selim kazanmıştır.

@Ecrin_Alara