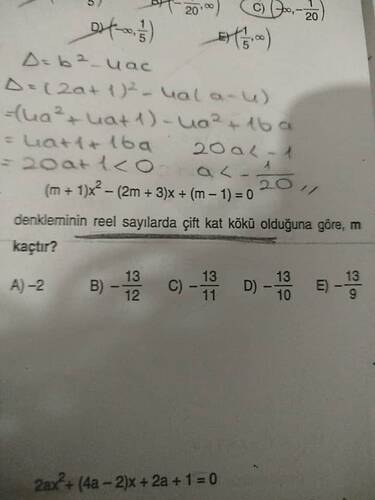Denkleminin reel sayılarda çift kat kökü olduğuna göre, ( m ) kaçtır?
Cevap:
Bir ikinci dereceden denklemin çift kat kökü olması için, diskriminantının ((\Delta)) sıfır olması gerekir. Bu durumda, diskriminantı hesaplayıp sıfıra eşitleyeceğiz.
Denklem:
[
(m+1)x^2 - (2m+3)x + (m-1) = 0
]
Çözüm Adımları:
-
Diskriminant Hesabı:
Diskriminant formülü:
[
\Delta = b^2 - 4ac
]Burada, (a = (m+1)), (b = -(2m+3)), (c = (m-1)).
[
\Delta = [-(2m+3)]^2 - 4(m+1)(m-1)
][
\Delta = (2m+3)^2 - 4(m+1)(m-1)
][
\Delta = 4m^2 + 12m + 9 - 4[(m^2 - 1)]
][
\Delta = 4m^2 + 12m + 9 - 4m^2 + 4
][
\Delta = 12m + 13
] -
Diskriminantın Sıfır Olması:
[
12m + 13 = 0
][
12m = -13
][
m = -\frac{13}{12}
]
Sonuç:
Bu denklemin reel sayılarda çift kat kökü olması için ( m = -\frac{13}{12} ) olmalıdır. Doğru cevap B şıkkıdır: (-\frac{13}{12}).