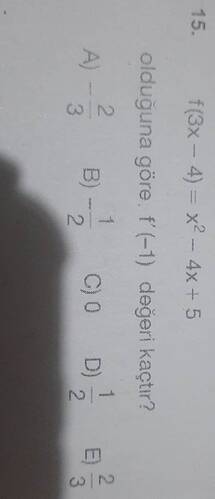Soru:
Verilen fonksiyon f(3x - 4) = x^2 - 4x + 5 olduğuna göre f(-1) değeri kaçtır?
Çözüm:
Fonksiyonu çözmek için x'i ve parametreyi yerine koyarken dikkatli olmalıyız. Verilen f(3x - 4) fonksiyonunda öncelikle girdiyle ilgili işlemleri adım adım uygulayacağız.
Adım 1: f(-1) için bağıntıyı çözmek
Fonksiyonda f(-1)'i bulmak istiyoruz. f(3x - 4) bağıntısına göre:
Adım adım ilerliyoruz:
- Doğrudan 3x - 4 yerine işlem yapmamız gerekiyor:
Şimdi 3x - 4 = -1 olacak şekilde çözümleyelim:
Adım 2: x = 1 değerini fonksiyona yerleştirme
x = 1 değerini verilen denklemde yerine koyarak f(-1)'i bulabiliriz:
x = 1 iken:
Cevap:
f(-1) değerimiz 2'dir.
Doğru seçenek: E) 2. ![]()
f(3x - 4) = x² - 4x + 5 olduğuna göre f’(-1) değeri kaçtır?
Cevap:
Öncelikle, verilen ifadenin türevini (x’e göre) alarak, fonksiyonun iç türeviyle (zincir kuralı) ilişkilendireceğiz. Adımları inceleyelim:
1. Zincir Kuralı Uygulama
Verilen ifade:
f(3x - 4) = x² - 4x + 5
Her iki tarafın x’e göre türevini alırsak:
d/dx [f(3x - 4)] = d/dx [x² - 4x + 5]
Zincir kuralı gereği sol tarafta:
f’(3x - 4) · (3x - 4)′ = f’(3x - 4) · 3
Sağ tarafın türevi:
(x² - 4x + 5)′ = 2x - 4
Bu durumda:
f’(3x - 4) · 3 = 2x - 4
Dolayısıyla:
f’(3x - 4) = (2x - 4) / 3
2. f’(-1) Değerini Bulma
f’(y) fonksiyonunu ‘y = 3x - 4’ formunda düşünüyoruz. Bize f’(-1) soruluyor, yani fonksiyonun türevi y = -1 değerinde.
3x - 4 = -1 ⇒ 3x = 3 ⇒ x = 1
x = 1 değerini yukarıdaki türev ifadesinde yerine koyalım:
f’(-1) = f’(3·1 - 4) = (2·1 - 4) / 3 = (2 - 4) / 3 = -2 / 3
Özet Tablosu
| Adım | İşlem | Sonuç |
|---|---|---|
| 1. Verilen ifade | f(3x - 4) = x² - 4x + 5 | - |
| 2. Her iki tarafın türevini al (x’e göre) | f’(3x - 4)·3 = 2x - 4 | f’(3x - 4) = (2x - 4)/3 |
| 3. y = -1 için 3x - 4 = -1 çöz | x = 1 | - |
| 4. f’(-1) değerini bul | f’(-1) = (2(1) - 4)/3 = -2/3 | -2/3 |
Sonuç olarak, f’(-1) = -2/3.