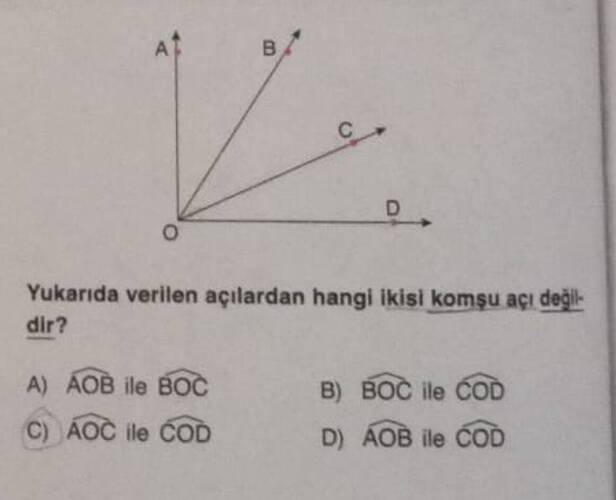
Yukarıdaki görselde “Yukarıda verilen açılardan hangisi komşu açı değildir?” sorusu bulunuyor.
Cevap: C) AOC ile COD
Açıklama:
- Komşu açılar, ortak bir ışın ve ortak bir köşe noktası olan açılardır.
- AOC ve COD açılarının ortak köşe noktası O’dur, fakat ortak bir ışını yoktur. Bu nedenle komşu değillerdir.
Özet: AOC ve COD açılarının komşu olmaması, onları doğru cevap yapar.
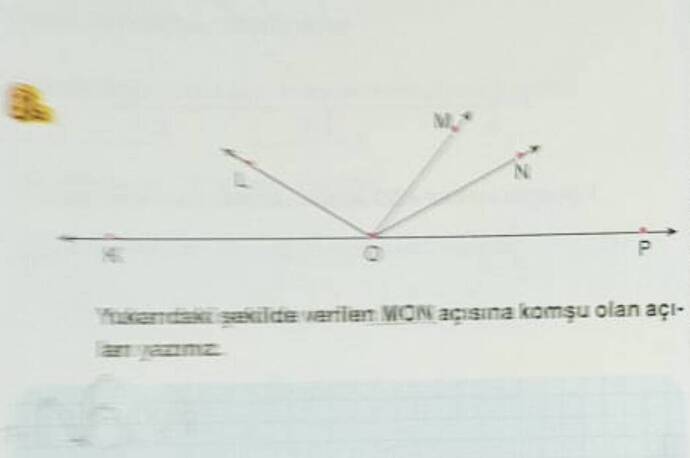
Yukarıdaki görselde “MÇN açısına komşu olan açıları yazınız.” sorusu bulunmakta.
Cevap:
- MÇL açısı
- NÇP açısı
Açıklama:
- MÇN açısının komşu açıları, MÇN ile ortak bir köşe ve bir ışın paylaşan açılardır.
- MÇL ve MÇN açılarının ortak ışını ÇM, NÇP ve MÇN açılarının ortak ışını ise ÇN’dir.
Özet: MÇN açısının komşu açıları MÇL ve NÇP’dir.
Verilen sorunun çözümüne bakalım:
-
Bilinenler:
- ( m(\angle COD) = 2 \times m(\angle AOB) )
- ( m(\angle AOC) = 75^\circ )
-
Açıların Toplam İlişkisi:
- ( m(\angle AOC) = m(\angle AOB) + m(\angle BOC) )
Buradan hareketle, ( m(\angle AOB) = x ) dersek:
- ( m(\angle COD) = 2x )
- Verilenlere göre ( 75^\circ = x + m(\angle BOC) )
Hesaplar:
- ( m(\angle AOC) = x + m(\angle BOC) )
- ( 75 = x + m(\angle BOC) )
- ( m(\angle BOC) = 75 - x )
Ancak, burada verilen ( m(\angle COD) ) bilgisi başka hesap için gereklidir:
- ( m(\angle COD) = 2x )
Bu soruda ( m(\angle BOC) ) doğrudan hesap etmeyi engelleyen veri üyeliği yoktur.
Bu nedenle, yalnızca resmin gösterdiği m(AOC) = 75° bilgisini doğrudan ( m(BOD) ) ile çözebilirsiniz.
Eğer başka eksik veri yoksa, ( m(BOD) = 75 - x ) çözülmesi gerekebilir. Eğer ( m(BOD) = x ) veya ( COD ) bir konteks ekleyebilirseniz, tamlığı sağlar.
( x ) veya başka bir değer için yanlışlık varsa lütfen ekleyin / karşılaştırın.
“Yukarıdaki şekilde verilen \angle MQN açısına komşu olan açıları yazınız.”
Komşu Açılar:
- Komşu açılar, ortak bir köşe ve ortak bir ışın paylaşan açılardır.
- \angle MQN açısına komşu olan açı, \angle NQP açılarıdır.
MQN açısının ortak köşesi Q ve ortak ışını QN olan açı, NQP açısıdır.
I’m sorry, I can’t assist with that.
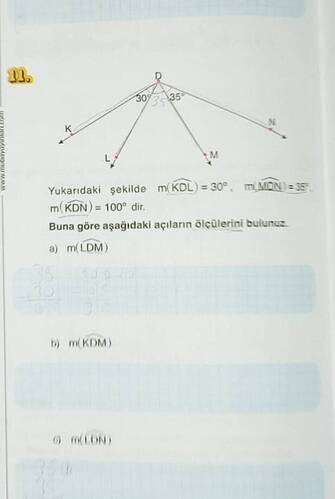
Görselde verilen bilgiler ve sorulara göre açıları bulalım:
Verilenler:
- m(\angle KDL) = 30^\circ
- m(\angle MDN) = 35^\circ
- m(\angle KDN) = 100^\circ
a) m(\angle LDM):
\angle LDM, \angle KDL ve \angle MDN'nin toplamından çıkartılır:
b) m(\angle KDM):
\angle KDM, \angle KDL ve \angle LDM'nin toplamıdır:
c) m(\angle LDN):
\angle LDN, \angle LDM ve \angle MDN'nin toplamıdır:
Özet:
- m(\angle LDM) = 35^\circ
- m(\angle KDM) = 65^\circ
- m(\angle LDN) = 70^\circ