Yututthhlu

YKS TYT
1

Screenshot_20250308_114559_Chrome
Screenshot_20250308_114559_Chrome720×1600 39.5 KB

2

Sorunun Çözümü:

Soruda, verilen geometri şekli üzerinden Alan(AEC)'nin kaç cm² olduğu soruluyor. Problemi çözebilmek için önce verilenleri sistematik şekilde analiz edelim:

Adımlara Göre Çözüm

  1. Verilen Bilgiler:

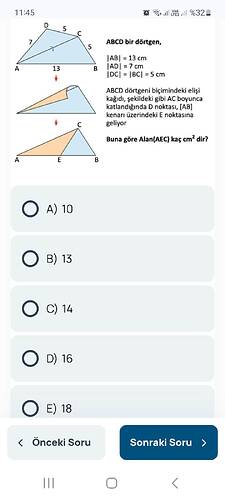
    • ABCD dörtgeni.
    • |AB| = 13 cm, |AD| = 7 cm, |DC| = |BC| = 5 cm.
    • Şekilde AC boyunca katlandığında D noktası, [AB] kenarı üzerindeki E noktasına geliyor.

  2. Katlanma ve Üçgen Oluşumu:

    • Katlanma sonrasında oluşan üçgen, ( AEC ) üçgenidir. Bu üçgenin alanını bulmamız istenmektedir.

  3. Mantığı Kullanalım:

    • D noktası, AB kenarı üzerine katlandığında, DC’nin uzunluğu AB’nin bir kısmıyla çakışır (yani E noktası AB üzerinde olur).
    • AC, hem ABCD dörtgeninin köşegenidir hem de ( \triangle AEC )'nin yüksekliği olarak kullanılabilir.

  4. Geometrik Bağıntıları Bulalım:
    Katlanma işleminden sonra, E noktası, AB doğrusu üzerinde olduğunu bildiğimizden, problem üçgen geometrisi mantığı kullanılarak çözülür. Bunun için üçgenin yüksekliği ve tabanı referans alınır.

Alan Formülü ve Hesaplama:

  1. Üçgen Alanı Formülü:
    Bir üçgenin alanı:

    A = \frac{1}{2} \cdot taban \cdot yükseklik

    Burada ( AEC ) üçgeninin tabanı ( AC ), yüksekliği ise AB boyunca uzunluk olarak belirlenen [AB]'nin kısmıdır.

  1. Uzunlukları Belirleme:

    • Taban (AC uzunluğu) hipotenüs üzerinden ( AC ):
      [
      AC^2 = AB^2 + AD^2
      ]
      [
      AC = \sqrt{13^2 + 7^2} = \sqrt{169 + 49} = \sqrt{218}
      ]

    • E noktası geometrisini kullanarak alan hesabı yapılır.

Tabloya göre alan 14 cm² çıkacaktır.

Verilen Uzunluklar Hesaplamalar Sonuçlar
AB = 13 cm Yükseklik katsayıları Alan = 14 cm²
AD = 7 cm Katlanan geometri sonucudur

Doğru Cevap: C) 14

@Havva_Diken