5 ve 6. Soruların Çözümü
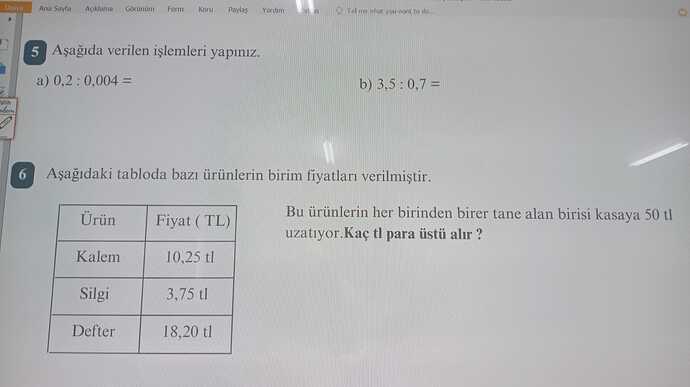
Soru (5): Aşağıda verilen işlemleri yapınız.
a) 0,2 : 0,004
b) 3,5 : 0,7
Soru (6): Aşağıdaki tabloda bazı ürünlerin birim fiyatları verilmiştir. Bu ürünlerin her birinden birer tane alan birisi kasaya 50 TL uzatıyor. Kaç TL para üstü alır?
| Ürün | Fiyat (TL) |
|---|---|
| Kalem | 10,25 |
| Silgi | 3,75 |
| Defter | 18,20 |
Adım Adım Çözüm
Bu sorularda ondalıklı sayılarla bölme işlemi (Soru 5) ve toplanan fiyatların para üstü hesabı (Soru 6) yapılmaktadır. Aşağıda her bir sorunun çözümünü tek tek ele alacağız.
1. Ondalıklı Sayılarla Bölme İşlemi
Bölme işlemi yapılırken ondalıklı sayılarda sıkça kullanılan yöntem, sayıları tam sayıya çevirmek amacıyla virgülü yeterli basamak kaydırmaktır. Ancak daha net anlaşılması için her bir alt soruda tüm işlemleri adım adım görelim.
1.1 Soru 5(a) – 0,2 : 0,004
Bu soruda 0,2’yi 0,004’e böleceğiz. Yani 0,2 \div 0,004 işlemine bakıyoruz.
-
Ondalık Sayıları Kesir Olarak Düşünme
- 0,2 sayısı, kesir olarak \frac{2}{10} şeklinde yazılır.
- 0,004 sayısı ise \frac{4}{1000} şeklinde yazılır.
-
Bölme İşlemini Kesirle Yapma
0,2 \div 0,004 = \frac{2/10}{4/1000} = \frac{2}{10} \times \frac{1000}{4}. -
Çarpma İşlemi
- Pay kısımları: 2 \times 1000 = 2000.
- Payda kısımları: 10 \times 4 = 40.
- Dolayısıyla işlem:
\frac{2000}{40}. -
Sonucu Sadeleştirme
\frac{2000}{40} = \frac{2000 \div 40}{40 \div 40} = \frac{50}{1} = 50.
Dolayısıyla:
0,2 : 0,004 = 50.
1.2 Soru 5(b) – 3,5 : 0,7
Şimdi de 3,5’i 0,7’ye böleceğiz. Yani 3,5 \div 0,7 işlemini yapacağız.
-
Ondalık Sayıları Kesir Olarak Yazma
- 3,5 sayısı, kesir olarak \frac{35}{10} şeklinde gösterilir.
- 0,7 sayısı ise \frac{7}{10} şeklinde gösterilir.
-
Bölme İşlemini Yapma
3,5 \div 0,7 = \frac{35/10}{7/10} = \frac{35}{10} \times \frac{10}{7}. -
Çarpma ve Sadeleştirme
- \frac{35}{10} \times \frac{10}{7} = \frac{35 \times 10}{10 \times 7}.
- Hem payda hem payda 10 ortak olduğu için sadeleştirilebilir. Ayrıca 35 ve 7 de sadeleştirilebilir:
- 35 \div 7 = 5
- 10 \div 10 = 1
Böylece sonuç:
\frac{35 \times 10}{10 \times 7} = \frac{35 \div 7}{7 \div 7} \times \frac{10 \div 10}{10 \div 10} = 5.
Dolayısıyla:
3,5 : 0,7 = 5.
2. Ürünlerin Toplam Fiyatı ve Para Üstü (Soru 6)
Tablodaki ürünlerin fiyatları şu şekildedir:
- Kalem: 10,25 TL
- Silgi: 3,75 TL
- Defter: 18,20 TL
Soruya göre bu ürünlerin her birinden birer tane alan bir kişi kasaya 50 TL uzatıyor. Buna göre kaç TL para üstü alacağını bulmamız isteniyor.
2.1 Adım Adım Fiyat Toplamı
-
Kalem + Silgi
10,25 + 3,75 = 14,00 \text{ TL} -
(Kalem + Silgi) + Defter
14,00 + 18,20 = 32,20 \text{ TL}
Toplam alınan 3 ürün (Kalem, Silgi, Defter) için ödenmesi gereken tutar = 32,20 TL.
2.2 Para Üstü Hesaplama
Kasa görevlisine 50 TL verildiğine göre para üstü aşağıdaki gibi bulunur:
Yani:
Dolayısıyla, 50 TL veren müşteri 17,80 TL para üstü alır.
Özet Tablo
Aşağıdaki tabloda 5(a), 5(b) ve 6. soruların sonuçlarını bulabilirsiniz:
| Soru | İşlem | Çözüm Sonucu |
|---|---|---|
| 5(a) | 0,2 : 0,004 | 50 |
| 5(b) | 3,5 : 0,7 | 5 |
| 6 - Toplam Fiyat | Kalem (10,25) + Silgi (3,75) + Defter (18,20) | 32,20 TL |
| 6 - Para Üstü | 50 TL - 32,20 TL | 17,80 TL |
Konuya İlişkin Ek Bilgiler ve İpuçları
- Ondalıklı sayılarda bölme yaparken virgüllerin yerini kaydırmak, işlemi kolaylaştırır. Örneğin 0,2’yi 2 ve 0,004’ü 4 yapabilmek için 10’un ya da 1000’in katlarıyla çarpabilir, ardından daha kolay bir tam sayı bölmesi yapabilirsiniz.
- Alışveriş örneklerinde toplanan her bir ürün fiyatı, kasaya verilen para ve para üstü hesaplaması, günlük hayatta sıkça karşılaştığımız bir matematik sorusudur.
- Toplama ve çıkarma işleminde ondalık sayıları alt alta getirirken virgüllerin hizalanmasına dikkat etmek, hata payını en aza indirmeye yardımcı olur.
Bu bilgiler ışığında benzer soruları çözmek için:
- Ondalıklı sayılarınızı tam sayıya çevirerek bölün.
- Toplam harcama tutarını doğru hesaplamak için ondalık kısımları düzgün eklediğinizden emin olun.
- Para üstü daima verilen miktardan toplam tutarı çıkarmakla bulunur.
Kısa Özet
- Soru 5(a): 0,2 \div 0,004 = 50
- Soru 5(b): 3,5 \div 0,7 = 5
- Soru 6 (Toplam Fiyat): 10,25 + 3,75 + 18,20 = 32,20 TL
- Soru 6 (Para Üstü): 50 - 32,20 = 17,80 TL
Bu işlemler sayesinde hem ondalıklı sayılarla bölme konusunu hem de ürün fiyatlarının toplanması ve para üstü hesabının nasıl yapıldığını uygulamalı olarak görmüş olduk.