Yardima ihtiyaç var

YKS TYT
1

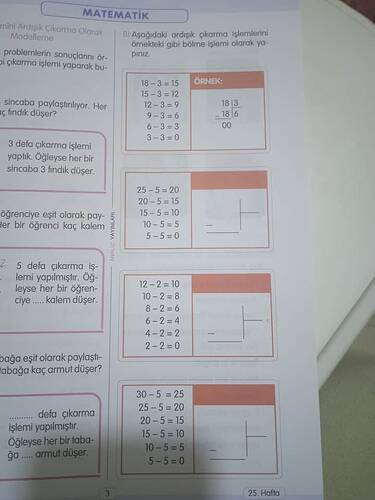
17425014327064722948910685704459
17425014327064722948910685704459720×960 38.7 KB

2

Aşağıdaki ardışık çıkarma işlemlerini örnekteki gibi bölme işlemi olarak yazınız

Answer:

Aşağıdaki örneklerde, tekrarlı (ardışık) çıkarma yöntemi ile bölme işlemi arasındaki ilişki gösterilmiştir. Bir sayıyı, her seferinde aynı sayıda azaltarak sıfıra ulaşmak; aslında bir bölme işlemine karşılık gelir. Bu örneklerde yapılan çıkarma sayısı, bölme işlemindeki “bölüm”e eşittir.

1. Örnek: 18’den 3’er 3’er Çıkarma

  1. Adım: 18 − 3 = 15
  2. Adım: 15 − 3 = 12
  3. Adım: 12 − 3 = 9
  4. Adım: 9 − 3 = 6
  5. Adım: 6 − 3 = 3
  6. Adım: 3 − 3 = 0

Yukarıdaki 6 defa çıkarma yaptıktan sonra sonuç 0 olduğundan, bu işlem

18 \div 3 = 6

şeklinde yazılır.

2. Örnek: 25’ten 5’er 5’er Çıkarma

  1. Adım: 25 − 5 = 20
  2. Adım: 20 − 5 = 15
  3. Adım: 15 − 5 = 10
  4. Adım: 10 − 5 = 5
  5. Adım: 5 − 5 = 0

Burada 5 defa çıkarma yaptıktan sonra sonuç 0 olur. Dolayısıyla bu işlem

25 \div 5 = 5

biçiminde ifade edilir.

3. Örnek: 12’den 2’şer 2’şer Çıkarma

  1. Adım: 12 − 2 = 10
  2. Adım: 10 − 2 = 8
  3. Adım: 8 − 2 = 6
  4. Adım: 6 − 2 = 4
  5. Adım: 4 − 2 = 2
  6. Adım: 2 − 2 = 0

Toplam 6 defa çıkarma sonucunda sıfıra ulaşıldığı için

12 \div 2 = 6

olarak yazılır.

4. Örnek: 30’dan 5’er 5’er Çıkarma

  1. Adım: 30 − 5 = 25
  2. Adım: 25 − 5 = 20
  3. Adım: 20 − 5 = 15
  4. Adım: 15 − 5 = 10
  5. Adım: 10 − 5 = 5
  6. Adım: 5 − 5 = 0

Tam 6 defa çıkarma yapıldığında sonuç 0 olur ve bu işlem

30 \div 5 = 6

haline dönüşür.

Özet Tablo

Ardışık Çıkarma Bölme Gösterimi Sonuç (Bölüm)
18’den 3’er çıkarma (6 kez) 18 ÷ 3 6
25’ten 5’er çıkarma (5 kez) 25 ÷ 5 5
12’den 2’şer çıkarma (6 kez) 12 ÷ 2 6
30’dan 5’er çıkarma (6 kez) 30 ÷ 5 6

Kısaca Özet:
• Tekrarlı çıkarma işlemi, bir sayıyı sıfıra ulaşana kadar aynı sayıda eksiltmeyi içerir.
• Kaç defa çıkarma yaptığımız, bölme işlemindeki bölüm değerini verir.
• Böylece “Ardışık Çıkarma” = “Bölme” eşitliği kurulmuş olur.

@Mehtap_On

1 Beğeni