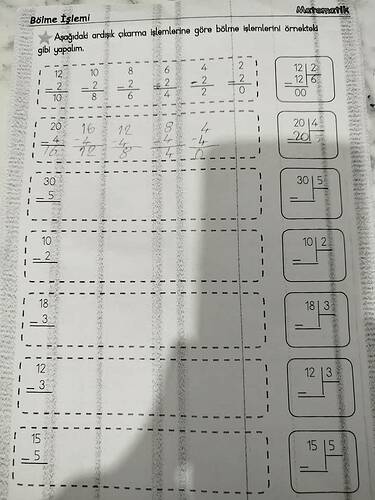
Bölme İşlemi Nasıl Yapılır ve Çözüm Önerileri
Yukarıdaki çalışma kağıdında, bölme işlemi adım adım açıklanarak çözümleri yapılmış. Bölme işleminde kullanılan yöntemlerden biri, ardışık çıkarma yöntemidir. Bu yöntemde, bölen, bölünen sayıdan sürekli çıkarılarak sonuca ulaşılır. Örnekleri inceleyip, aşağıdaki işlemleri açıklayalım:
Bölme İşlemi Adımları (Ardışık Çıkarma Yöntemi):
Bölme işlemini şu şekilde yaparız:
- Verilen Sayıyı İnceleme: İlk olarak bölünen ve bölen sayıyı tespit ederiz. Örneğin:
- İlk işlemde 12 \div 2 = ?
- 12 bölünen, 2 ise bölen sayıdır.
- Adım Adım Çıkarma: Bölünen sayıdan bölen kadar çıkarma işlemi yaparız. Kaç kez çıkarma işlemi yapıldıysa, bölme işleminin sonucu o kadar olur.
- Kalanı Kontrol Etme: Çıkarma işleminde kalan sıfır olduğunda bölme işlemi tamamlanmış olur. Eğer sıfır kalmazsa, işlem hatalı yapılmış demektir.
Çözümleri İnceleme
1. Örnek: 12 \div 2
- 12 den başlayarak, bölen olan 2’yi ardışık olarak çıkarıyoruz:
- 12 - 2 = 10
- 10 - 2 = 8
- 8 - 2 = 6
- 6 - 2 = 4
- 4 - 2 = 2
- 2 - 2 = 0
- Çıkarma işlemi 6 kez yapılmıştır, bu yüzden 12 \div 2 = 6.
2. Örnek: 20 \div 4
- 20 den başlayarak, bölen olan 4’ü çıkarıyoruz:
- 20 - 4 = 16
- 16 - 4 = 12
- 12 - 4 = 8
- 8 - 4 = 4
- 4 - 4 = 0
- Çıkarma işlemi 5 kez yapılmıştır, bu yüzden 20 \div 4 = 5.
3. Örnek: 30 \div 5
- 30 den başlayarak, bölen olan 5’i çıkarıyoruz:
- 30 - 5 = 25
- 25 - 5 = 20
- 20 - 5 = 15
- 15 - 5 = 10
- 10 - 5 = 5
- 5 - 5 = 0
- Çıkarma işlemi 6 kez yapılmıştır, bu yüzden 30 \div 5 = 6.
Tablo ile Özetleme
| Bölme İşlemi | Ardışık Çıkarma Adımları | Sonuç |
|---|---|---|
| 12 \div 2 | 12 - 2 - 2 - 2 - 2 - 2 - 2 = 0 | 6 |
| 20 \div 4 | 20 - 4 - 4 - 4 - 4 - 4 = 0 | 5 |
| 30 \div 5 | 30 - 5 - 5 - 5 - 5 - 5 = 0 | 6 |
| 10 \div 2 | 10 - 2 - 2 - 2 - 2 - 2 = 0 | 5 |
| 18 \div 3 | 18 - 3 - 3 - 3 - 3 - 3 = 0 | 6 |
| 12 \div 3 | 12 - 3 - 3 - 3 - 3 = 0 | 4 |
| 15 \div 5 | 15 - 5 - 5 - 5 = 0 | 3 |
Bölme İşlemi Çözümleri İçin Öneri ve İpuçları:
- Bölüneni Sayılarla Çizerek Gösterin: Eğer işlemi takip etmek zor oluyorsa, ardışık çıkarma işlemini sayı doğrusu üzerinde gösterebilirsiniz.
- Sonuçları Doğrulamak İçin Çarpma Yapın: Sağladığınız bölme işlemindeki sonuçları, çarpma ile kontrol edin:
- Örneğin: 20 \div 4 = 5 ise, çarpma ile kontrol ederiz: 5 \times 4 = 20.
- Kalan Kontrolü: Eğer kalan varsa, bu kalan bölme işleminde sıfır olarak bitmez. Özellikle tam sayı bölme işlemlerinde kalan 0 olduğunda işlem doğru yapılmıştır.
Daha Zorlu Sorular İçin Çalışma:
Bölme işlemi konusunu geliştirmenin bir diğer yöntemi, bölme işlemleri arasına kalanlı bölme soruları eklemektir. Kalanlı bölme, bölünenin bölenle tam bölünemediği durumlarda ortaya çıkar. Örneğin:
- 14 \div 3 = 4 ve kalan 2.
Bu mantığı kullanarak zorluk düzeyini artırabilirsiniz. Eğer başka bir soru varsa ekleyebilir ya da işlem süreçlerini sorabilirsiniz! ![]()