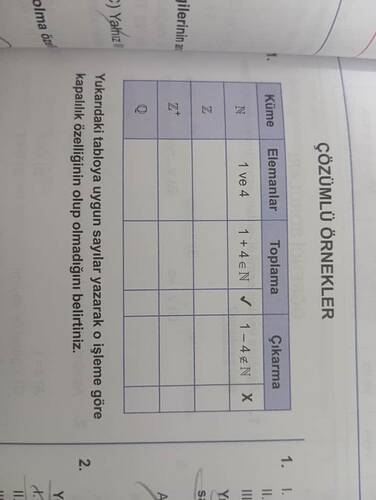
Yukarıdaki tablodaki işlemlere göre küme kapalı mı?
Tablo, belirli sayılar ve kümeler için toplama ve çıkarma işlemlerinin kapalı olup olmadığını göstermektedir. Kapalılık, matematikte bir kümenin belirli bir işlem altında kapalı olması demektir; yani, işlem iki eleman üzerinde uygulandığında sonuç yine aynı kümede kalıyorsa, o işlem için küme kapalıdır.
Tablo Analizi
- Kümeler ve İşlemler:
- Q (Rasyonel Sayılar):
- Toplama: “1 ve 4” elemanları üzerinden inceleyeceğiz. Eğer 1 + 4 işlemi rasyonel bir sayı veriyorsa, toplama işlemi Q kümesi için kapalıdır.
- Çıkarma: Aynı şekilde “1 - 4” işlemi üzerinden değerlendirilir.
- Z⁺ (Pozitif Tam Sayılar):
- Toplama: Pozitif tam sayıların toplandığında sonuç yine pozitif tam sayı ise, toplama işlemi Z⁺ için kapalıdır.
- Çıkarma: Eğer çıkarma işlemi pozitif sonuç verirse, çıkarma Z⁺ için kapalıdır.
- Z (Tam Sayılar):
- Toplama: Tam sayıların toplamı yine tam sayı ise kapalıdır.
- Çıkarma: Tam sayıların farkı yine tam sayı veriyorsa kapalıdır.
- N (Doğal Sayılar):
- Toplama: Doğal sayıların toplamı yine doğal sayı ise kapalıdır.
- Çıkarma: Doğal sayılardan birinin diğerinden çıkarılması sonucu negatif olursa, bu küme kapalı değildir.
- Q (Rasyonel Sayılar):
Çözümler ve Sonuçlar
-
Q (Rasyonel Sayılar):
- 1 + 4 = 5 (\in) Q, kapalı
- 1 - 4 = -3 (\in) Q, kapalı
-
Z⁺ (Pozitif Tam Sayılar):
- 1 + 4 = 5 (\in) Z⁺, kapalı
- $1 - 4 = -3 \not\in ) Z⁺, kapalı değil
-
Z (Tam Sayılar):
- 1 + 4 = 5 (\in) Z, kapalı
- 1 - 4 = -3 (\in) Z, kapalı
-
N (Doğal Sayılar):
- 1 + 4 = 5 (\in) N, kapalı
- $1 - 4 = -3 \not\in) N, kapalı değil
Sonuç olarak, toplama işlemi için tüm kümeler kapalı iken çıkarma işlemi için yalnızca Q ve Z kümeleri kapalıdır. Kapalı olmayanlar ilgili hücrelerde “X” ile gösterilmiştir.
Bu bilgi, kapalı küme işlemlerinin anlaşılması noktasında oldukça bilgilendirici bir örnek teşkil eder. Matematikte kullanılan kümeler ve işlemlerle çalışırken, bu tür bilgileri dikkatli bir şekilde değerlendirmek, daha karmaşık problemlerin çözümünde de yol göstericidir.