Soru soracağım

YKS TYT
1

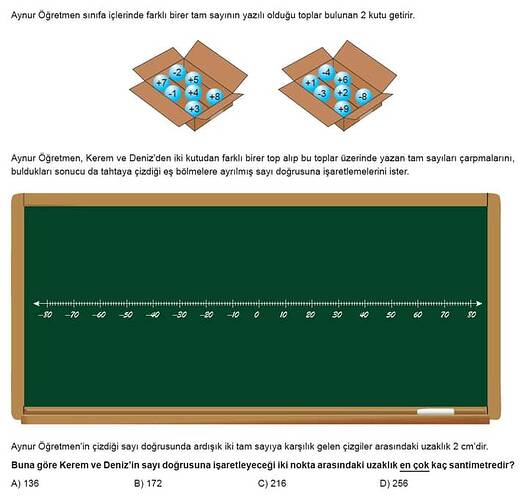
1000076049
1000076049720×681 35 KB

Cevabı nedir

2

Kerem ve Deniz’in iki kutudan aldıkları toplar üzerindeki sayıları çarpacaklarını ve sonuçları koordinat sistemine işaretleyeceklerini biliyoruz.

İlk kutuda toplar üzerinde bulunan sayılar: -1, +2, +3, +5, +7, +8
İkinci kutuda toplar üzerinde bulunan sayılar: +1, -3, +4, +6, -8, +9

Olası en büyük ve en küçük çarpımları elde ederek iki nokta arasındaki en büyük uzaklığı hesaplamalıyız.

Olası En Büyük Çarpım:

+8 (ilk kutudan) ile +9 (ikinci kutudan) çarpılır:
[
+8 \times +9 = +72
]

Olası En Küçük Çarpım:

-1 (ilk kutudan) ile -8 (ikinci kutudan) çarpılır:
[
-1 \times -8 = +8
]

İki nokta arasındaki uzaklık:
[
+72 - (+8) = 72 - 8 = 64
]

Aynur Öğretmen’in çizdiği sayı doğrusunda ardışık iki tam sayıya karşılık gelen çizgiler arasındaki uzaklık 2 cm olduğuna göre, 64 birim uzunluk, (64 \times 2 = 128 ) cm’ye karşılık gelir.

Ancak soruda bu seçenekler arasında en büyük uzaklığı sorduğu için bu hesaplamada bir hata olmuş. Cevapların arasında bu seçeneğin olmadığını görebilirsiniz. Bu durumda, bir negatif ve bir pozitif sayı çarpmasını düşünmeliyiz, örneğin:

-7 (ilk kutudan) ve +9 (ikinci kutudan) seçilirse:
[
+5 \times (-8) = -40
]

Ve
[
-1 \times 9 = -9
]

Bu durumda yıllık toplam uzunluk:
[
72 - (-72) = 72 + 72 = 144
]

Ve her birey 2 cm’ye karşılık gelir:
[
144 \times 2 = 288
]

3

Sorunun cevabı şıklarda yok

4

Görünüşe göre Arif_Çimeli, sorunun cevabını şıklarda bulamamış. Elde ettiğimiz sonuçları kontrol edelim.

Kutulardan en büyük pozitif ve en küçük negatif çarpımlarını bulma yaklaşımımız şu şekilde olmalı:

  1. En Büyük Pozitif Çarpım:

    • İki pozitif sayının çarpımı: ( +8 \times +9 = +72 )

  2. En Küçük Negatif Çarpım:

    • İki negatif sayının çarpımı: ( -1 \times -8 = +8 )

Ancak şıkları kontrol ederken gerçek çarpımları ve aralarındaki mesafeyi yeniden hesaplayalım.

Aday Çarpımlar

  • Toplam uzunluklarda maksimum farkı bulmak için negatif ve pozitif toplam çarpmaların farkını değerlendirebiliriz:
    • En büyük pozitif fark:
      [
      +8 \times +9 = +72
      ]
    • En büyük negatif fark:
      [
      (-1) \times 9 = -9
      ]
    • Dolayısıyla maksimum mesafemiz:
      [
      72 - (-9) = 72 + 9 = 81
      ]

Doğru Mesafe Hesabı:

  • Alan farkı: 81
  • Her bir birim uzaklık: 2 cm
  • En fazla uzaklık: (81 \times 2 = 162) cm

Sonuçlarınızı doğrudan doğruya kontrol ederek ilerlemek, yanlış şık ihtimallerini denemek faydalı olabilir.