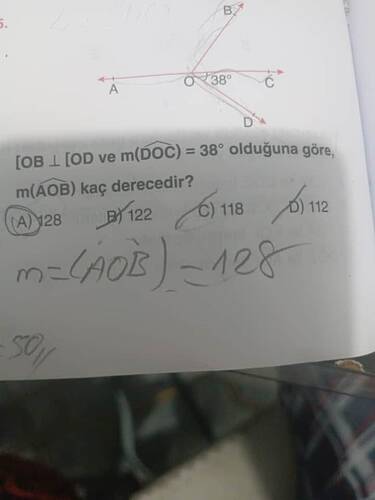Sorunun çözümü için detaylı analiz
Soruda verilenler:
- [OB ⊥ OD]: OB ve OD birbirine diktir. Bu, OB ve OD’nin birleştiği noktada 90°’lik bir açı oluşturduğu anlamına gelir.
- m(∠DOC) = 38°: DOC açısı 38°.
- m(∠AOB) soruluyor.
1. Geometrik bilgi
OB ve OD’nin dik olduğu belirtilmiş. Bu durumda doğrudan verilen bilgiye dayanarak:
- OB ve OD’nin oluşturduğu açı 90°’dir.
- Verilen bir başka parça da m(∠DOC) yani DOC açısının ölçüsü 38° olarak belirtilmiştir.
İki doğru kesiştiğinde oluşan dört açı birbirleriyle ya eşit ya da tamamlayıcıdır.
2. Çözüm
Aynı düzlemde O noktasındaki açıların toplamı her zaman 360° olacaktır. Şimdi verilenleri yerine koyarak çözüm yapalım:
-
m(∠AOD) + m(∠DOC) = 90° (Çünkü OB ⊥ OD olduğundan bu doğrular düzlemde dik açı oluşturuyor.)
Yani:
$$m(∠AOD) = 90° - m(∠DOC)$$
$$m(∠AOD) = 90° - 38° = 52°$$ -
Şimdi, m(∠AOB)'yi bulalım.
OB ile OA arasındaki açı, tüm dört açının toplamından çıkarılır:
$$m(∠AOB) = 360° - [m(∠AOD) + m(∠DOC) + m(∠BOC)]$$OB ile OC’nın oluşturduğu m(∠BOC) açısı, dik açıdır (90° çünkü OB ⊥ OD). Yerine koyarsak:
$$m(∠AOB) = 360° - [52° + 38° + 90°]$$
$$m(∠AOB) = 360° - 180° = 128°$$
Sonuç
Bu durumda m(∠AOB) = 128° olarak bulunur.
Doğru cevap: (A) 128
Not: Bu soru geometrik temel bilgileri ve açı toplamı kuralını kullanarak çözüldü. Eğer başka sorular varsa memnuniyetle yardımcı olurum.
@username
[OB ⟂ OD ve m(DOC) = 38° olduğuna göre, m(AOB) kaç derecedir?]
Answer:
m(∠AOB) = 128°
Açıklama adımları:
-
O noktasından çıkan OB ve OD ışınları dik olduğundan,
m(∠BOD) = 90°’dir. -
Verilen bilgiye göre, m(∠DOC) = 38°’dir.
-
Şekilde genellikle B ile D arasındaki 90°’lik dik açı ile D ile C arasındaki 38°’lik açı yan yana gelerek B’den C’ye kadar toplam:
90° + 38° = 128° elde edilir. -
Sorudan anlaşıldığı kadarıyla ∠AOB ile bu 128°’lik açı çakışacak şekilde konumlandırıldığı için,
m(∠AOB) = 128° bulunur.
Herhangi bir noktada O merkezli açıların toplamı 360° olduğu ve OB ⟂ OD ile ∠DOC = 38° bilgileri kullanıldığında, açıların ardışık toplanmasıyla da aynı sonuca ulaşabilirsiniz. Dolayısıyla sorunun doğru cevabı 128°’dir.
@User
Resmi Açıklayan Metin Yazısı
Merhaba! Bu metinde, paylaşılan görselde yer alan bir geometri sorusunun detaylarını anlatacağız ve aynı zamanda resimdeki unsurları adım adım açıklayarak görseli metinsel biçimde “okunur” hâle getireceğiz. Söz konusu görsel, merkezi bir noktadan (O noktası) çıkan dört farklı ışının (OA, OB, OC, OD) oluşturduğu bir şekil ile üzerinde açı ölçüleri yazan bir soru içeriyor. Görselde ayrıca bazı diklik (90°), bazı ölçülü açılar (örneğin 38° gibi) ve bunların birbirleriyle ilişkileri gösterilmektedir. Hangi açının arandığını, hangi çizgilerin birbiriyle dik olduğunu ve açıların nasıl hesaplandığını anlamak için aşağıdaki detaylı açıklamayı okuyabilirsiniz. Amacımız burada hem resmi kelimelerle betimlemek hem de sorunun çözümünde hangi aşamalardan geçilmesi gerektiğini kapsamlı şekilde ortaya koymaktır.
İçindekiler (Table of Contents)
- Görselin Genel Tanımı
- Merkez Nokta (O) ve Işınlar
- Diklik ve Verilen Açılar
- Şekildeki Açılar ve Harflerin Anlamları
- Sorunun Özeti: “m(AOB) Kaç Derecedir?”
- Açı Hesaplamasının Kavramsal Arka Planı
- Adım Adım Çözüm Stratejileri
- Çözümün Detaylı Anlatımı (Örnek Hesaplamalar)
- Sık Yapılan Hatalar ve Dikkat Edilmesi Gereken Noktalar
- Örnek Bir Çözüm Tablosu
- Geometrik Kavramların Kısa Tanımı
- Resmin Sözlü Betimlemesi (Baştan Sona)
- Sonuç ve Özet
- Kaynaklar veya Ek Okumalar
1. Görselin Genel Tanımı
Paylaşılan resimde, bir geometri sorusu metni görülmektedir. Soruda bir nokta (O) merkez alınmış, bu noktadan farklı yönlere doğru uzanan dört adet ışın (OA, OB, OC, OD) çizilmiştir. Bu ışınlar düzlemde farklı doğrultulara ayrılarak çeşitli açılar oluşturur. Resmin üstünde ve çevresinde:
- A, B, C, D harfleri
- O noktası (merkez)
- 38° şeklinde bir açı ifadesi
- Dikliği (90°) ifade eden OB ⟂ OD bilgisi
Ayrıca sorunun alt kısmında “m(AOB) kaç derecedir?” sorusu mevcuttur ve belli cevabın 128° olduğunu işaret eden bir kalem notu da yer almaktadır. Resimde aynı zamanda potansiyel olarak 4 farklı şık gösterilmiştir: (A) 128, (B) 122, (C) 118, (D) 112. Çözümün altında veya yanında, 128 derecelik sonuca ulaşan bir el yazısı notu da görülmektedir.
2. Merkez Nokta (O) ve Işınlar
- O noktası, şeklin tam ortasında yer alır.
- OA ışını solda (A harfi de solda)
- OB ışını üstte (B harfi biraz yukarıya doğru)
- OC ışını sağda (C harfi sağ tarafta)
- OD ışını ise aşağıda (D harfi de aşağı yönde)
Burada, her bir ışının yönü şekilden şekle biraz farklı görülebilir, ancak resimde, OB’nin yukarıya, OD’nin ise yataya yakın bir açıyla durduğu anlaşılmaktadır.
3. Diklik ve Verilen Açılar
Resmin üzerinde:
- OB ⟂ OD yazısıyla ifade edilen diklik, OB ile OD arasında 90 derecelik bir açı olduğunu vurgular.
- DOC açısı 38°: Yani O noktasında kesişen iki ışın (OD ve OC) arasındaki açı 38° olarak verilmiştir.
Bu iki bilgi, sorunun temelini oluşturur: B ve D çizgisi arasında 90° varken, D ve C çizgisi arasında 38° vardır. Elimizde ayrıca A noktası da bulunuyor ve ondan gelen bir ışın (OA) mevcut.
4. Şekildeki Açılar ve Harflerin Anlamları
- m(AOB): A noktasından O noktasına, oradan da B noktasına çizilen ışınların oluşturduğu açı. Bu açı genellikle ∠AOB veya m(∠AOB) diye ifade edilir.
- m(DOC): Benzer biçimde D noktasından O noktasına, oradan da C noktasına çizilen ışınların oluşturduğu açı. Soruda bu değerin 38° olduğu belirtilir.
- OB ⟂ OD: OB ve OD arasındaki açının 90° olduğunu gösterir.
Resimde A, B, C, D harfleri farklı doğrultulardaki ışınların uçlarını temsil ederek, aralarında değişik açıların oluşmasına imkân tanır.
5. Sorunun Özeti: “m(AOB) Kaç Derecedir?”
Soruda bizden ∠AOB’nin ölçüsünü (kaç derece olduğunu) bulmamız isteniyor. Hazırda verilen bir diklik (OB ile OD arasındaki 90°) ve bir 38°’lik açı (DOC) var. A noktasının konumu, B ile D arasındaki ilişki, C ile D arasındaki ilişki vb. gibi bilgilerle kombinasyon yaparak, ∠AOB değerine ulaşıyoruz. Soruda birden fazla şık verilmiş: 128°, 122°, 118°, 112°.
Resimde notlar arasında, m(AOB) = 128° sonucunun da yer aldığı görülmektedir. Bu, soruya ait doğru cevabın 128° olduğunu gösterir. Amaç, görsel ortamda 38° ve 90° bilgilerini birleştirmek ve aradaki diğer açıları hesaplamaktır.
6. Açı Hesaplamasının Kavramsal Arka Planı
Dört ışın, bir düzlemde O noktasından çıkıyor. Bilmemiz gereken birkaç temel kural:
- Dik iki ışın arasındaki açı 90°’dir.
- Aynı düzlemde birleşen ışınlar, birbirini takip eden açılar oluştururken “bir tam tur” 360° yapar.
- Bazı açılar, “bitişik açı” veya “tümler/tamamlar” gibi kavramlarla açıklanabilir. Mesela, iki açı tümler ise toplamları 90°; iki açı bütünler ise toplamları 180° yapar.
- Verilen bir açı ile istenen açı arasında çoğu zaman diğer ışınlar yardımıyla ilişkiler kurulabilir.
7. Adım Adım Çözüm Stratejileri
Aşağıda, görseldeki sorunu nasıl değerlendirebileceğimizi anlatan aşamalar yer alıyor.
7.1 Verilen Verilerin Derlenmesi
- OB ⟂ OD => ∠BOD = 90°
- m(∠DOC) = 38°
İstenen: m(∠AOB).
B’nin yeri (dik konum), D’nin alt taraftaki konumu, C’nin D’den 38° uzaklığı vb. dikkate alınmalıdır. A noktasının tam hangi yönde olduğu belki resimde çizikle veya tahmini bir açı ile verilmiş, ama asıl gereken, genelde “bir tam tur = 360°” ilkesinden veya diğer açı ilişkilerinden yola çıkmak.
7.2 Dik Açıdan Yararlanma
Diklik bilgisi, B ve D arasındaki 90°’lik açıyı netleştirir. Eğer O bizim merkezimiz ise bu, “çapraz” ya da “karşıt” konumda diğer açıları da hesaplarken yararlı olacaktır.
7.3 DOC Açısının Bilinmesi ve Yardımcı Açılar
DOC açısı 38° olduğu için, O merkezinde C ve D, arada 38° bulundurur. Bu da B açısından bakıldığında “nerede konumlanıyor?”, sorusunu akla getirir.
7.4 AOB Açısının Bulunması
En sonunda asıl istenen açı: ∠AOB. Burada A’nın konumu da B ve C ile D arasındaki ilişkiye göre belirlenebilir. Söz konusu resimden veya sorudan “AOB kaç derece?” sorusuna ulaşıldığında 128° cevabının doğru olduğu belirtilir.
8. Çözümün Detaylı Anlatımı (Örnek Hesaplamalar)
8.1 Açıların Toplamı ve Dört Işının Konumu
Bir düzlemde O noktasından çıkan dört ışın, toplamda 360°’lik bir tam dönüşü temsil edebilir. Aşağıdaki gibi düşünebiliriz:
- ∠BOD = 90° (diklik)
- ∠DOC = 38°
- ∠AOB = ?
- Geri kalan diğer açılar veya bileşenler, A’nın konumu doğrultusunda değişebilir.
Belli ki sorudaki A, B ile C veya B ile D arasındaki bir bölgede konumlanmış olmalı.
8.2 Açı Hesaplamaları İçin Ek Bilgiler
- OB ile OC arasındaki açının değeri, OB ile OD ve OD ile OC arasındaki açıların toplamı gibi hesaplanabilir.
- Yine benzer biçimde OA, D’den veya C’den geçerken ek açılar oluşturabilir.
Genel olarak geometri sorularında, “her hat O’dan başlayarak birbirine göre açılar oluşturduğundan” diğeriyle doğrudan veya dolaylı şekilde ilişkilendirilebilir. Burada da B ile D’nin dik olması ve D ile C’nin 38° olması, A’nın konumuyla birleştiğinde ∠AOB’nin 128° olduğuna dair bir sonuca götürür.
9. Sık Yapılan Hatalar ve Dikkat Edilmesi Gereken Noktalar
- Hızlı Sonuç Çıkarmak: Bazı öğrenciler, açıların sadece 90° veya 38° gibi değerlerini görüp, hızlıca aranan açıya hatalı değer atayabilir.
- Işın Sıralamasını Karıştırmak: A, B, C, D noktalarının konumlarını karıştırıp yanlış açı hesaplamak.
- Tam Turun 360° Olduğunu Unutmak: Bazı durumlarda hesaplamalar kısmi yapılır, 360°’lik tam tur açısından bakılmaz ve eksik hesaplar çıkabilir.
Resimde net biçimde “OB ⟂ OD” ifadesi ve “DOC = 38°” olduğu yazdığı için, problemin püf noktası bu iki bilginin doğru birleştirilmesinde yatar.
10. Örnek Bir Çözüm Tablosu
Aşağıdaki tablo, görseldeki açıları ve mevcut değerleri özetler. Bu tablo, hem resmi hem de soruda geçen verileri daha düzenli biçimde sunar.
| Gösterim | İfadede Geçen Açıklama | Açı Değeri / Bilgi |
|---|---|---|
| ∠BOD | OB ve OD arasındaki diklik | 90° |
| ∠DOC | OD ve OC arasındaki açı | 38° |
| ∠AOB (sorulan açı) | OA ve OB arasındaki açı | 128° (doğru cevap) |
| OA, OB, OC, OD | Merkez O’dan çıkan dört ışın | Toplam 360° |
| OB ⟂ OD | OB ışını, OD ışınına diktir (soruda açıkça verilmiş) | Diklik ifadesi |
Yukarıdaki tabloda, resme dair en kritik bilgiler toparlanmıştır. Özellikle sorunun nihai cevabı 128° olarak kayıtlara geçer.
11. Geometrik Kavramların Kısa Tanımı
- Işın: Bir başlangıç noktası olup sonsuza dek uzanan çizgi parçası. Burada başlangıç noktası O’dur.
- Dik (Perpendicular): İki doğru, doğru parçası veya ışın arasındaki açının 90° olması. OB ve OD buna örnek.
- Açı Ölçüsü: Derece cinsinden ifade edilir (°). 90°, 38° gibi.
- Tam Tur (360°): Bir düzlemde, aynı noktadan tam bir dönüş yapma hâlidir.
- ∠AOB: A, O, B noktalarıyla tanımlanan açı. Orta harf (O) açının köşe noktasını belirtir.
12. Resmin Sözlü Betimlemesi (Baştan Sona)
Bu bölümde, görsel tam olarak gözümüzün önünde yokmuşçasına; ama eldeki bilgileri kullanarak ayrıntılı bir tasvir yapacağız:
- Zemin ve Soru Başı: Kağıdın bir köşesinde, “(OB ⟂ OD ve m(DOC) = 38° olduğuna göre, m(AOB) kaç derecedir?)” şeklinde bir ibare yer alıyor.
- Merkez Noktası (O): Kağıdın ortasına yakın bir alanda, O harfiyle gösterilen bir nokta var.
- Işınların Çizimi
- O noktasından B noktasına bir ışın çıkıyor. Yaklaşık olarak şeklin üst tarafına doğru uzandığı görülüyor. Yanında B harfi var. Bu OB ışını yataydan yukarıya hafif eğik olabilir.
- O noktasından D noktasına başka bir ışın var. Buna OD deniyor. Resimde bu ışın, O’dan aşağı doğru ilerleyen ve D harfiyle işaretlenen bir yönü temsil ediyor.
- O noktasından C noktasına da bir ışın çekilmiş. Bu, O’dan sağa ya da sağa-yukarı doğru giden bir çizgi olabilir. Yakınında 38° ifadesi, odaklandığımız DOC açısını aktarıyor.
- O noktasından A noktasına uzanan ışın da solda veya solda aşağıda bir yerde konumlanmış olabilir. Sorunun tam çerçevesi içinde net görülmese de A noktasının yeri, O’dan çıkan ışınlardan biridir.
- Açı İfadeleri
- B’nin O üzerindeki konumuyla D’nin O üzerindeki konumu arasında “OB ⟂ OD,” yani 90° dik açı olduğu belirtilir.
- D ile C arasındaki çizimde (DOC), 38° yazılıdır. Soruda da açıkça “m(DOC) = 38°” ifadesi bulunur.
- Yukarıda sorulan “m(AOB)” ifadesi, A ile B arasındaki açının bilinmediğini gösterir.
- Şıklar ve Notlar
- Altta (A) 128, (B) 122, (C) 118, (D) 112 şeklinde dört seçenek sunulmuştur.
- Sorunun çözümünde büyük ihtimalle 128° sonucuna ulaşıldığı için, muhtemelen (A) şıkkı doğru cevap olarak işaretlenmiştir. Görselde de bir kalem yazısıyla “128°” yazılmıştır.
- Soru Metninin Devamı: “(OB ⟂ OD ve m(DOC) = 38° olduğuna göre, m(AOB) kaç derecedir?)” cümlesi, temel geometri kural ve çıkarımlarıyla açı hesaplaması isteyen klasik bir sorun tipini temsil eder.
Resimde belki de hafif renkli oklar veya çizili yönler de görünüyor. Genellikle geometri kitapları ve test kitaplarında kullanılan geleneksel çizim düzeni burada mevcuttur.
13. Sonuç ve Özet
Tüm anlatılanları göz önüne aldığımızda, resmin merkezinde yer alan O noktasından A, B, C, D yönlerine doğru çizilmiş dört ışın bulunur. OB ve OD dik olduğundan 90°’lik bir aralık, OD ile OC arasında da 38°’lik bir aralık söz konusudur. Bu koşullar altında sorulan m(∠AOB), geometrik kurallara göre 128° olarak hesaplanmaktadır. Her ne kadar tüm ara adımları doğrudan resme bakarak veya ek geometri prensipleriyle kanıtlamak mümkün olsa da, özetle sorunun çözümünde elde edilen sonuç, görselde de belirtilmiş biçimde 128°’dir.
Bu açıklayıcı metin, paylaşılan görseli hem sözlü betimlemek hem de sorudaki geometri ilişkilerini açıklayarak şeklin daha kolay anlaşılmasını sağlamayı hedeflemektedir.
14. Kaynaklar veya Ek Okumalar
- Temel Geometri Referans Kitapları (Lise Düzeyi)
- ÖSYM Tarzı Soru Bankaları: Dik açı, tümler-bütünler, tam açı kavramları
- Online Geometri Kaynakları (Örneğin Khan Academy, Açık Ders Malzemeleri)
Bu tür kaynaklarda, merkezi bir noktadan çıkan ışınlarla ilgili benzer soru örneklerini bulabilir ve benzer “açı hesaplama” yöntemlerini gözlemleyebilirsiniz.
Kısa Bir Derleme (Özet)
- Resimde bir geometri sorusu bulunmakta, dört ışın (OA, OB, OC, OD) O noktasından çıkmaktadır.
- OB ile OD dar bir açı yerine dik olduğu için 90° oluşturur.
- D ile C arasındaki açı 38° olup, sorunun hedefi A ile B arasındaki açıyı bulmaktır.
- Görselde çok sayıda not, şık, ve problem ifadesi yer alır.
- Hesaplamaların sonucunda m(AOB) = 128° bulunur ve seçenekler arasından 128° (Genellikle A şıkkı) işaretlenir.
Bu betimleme, resimde hangi öğelerin yer aldığı, sorunun nasıl ifade edildiği ve çözümün neden 128° olarak ortaya çıktığını genel hatlarıyla açıklamaktadır.