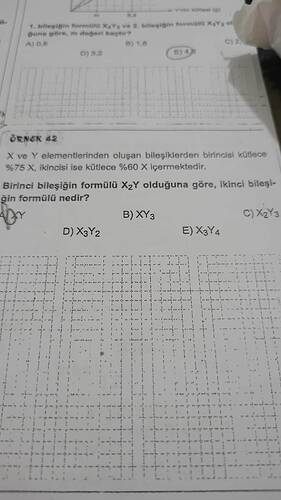
Örnek 42’yi çözmek için aşağıdaki adımları izleyelim:
Verilenler:
- Birinci bileşik %75 X içeriyor ve formülü X_2Y.
- İkinci bileşik %60 X içeriyor ve formülü bilinmiyor.
1. Birinci Bileşiğin Analizi:
Formül X_2Y olduğuna göre, mol kütleleri açısından:
- X_2Y: 2 birim X ve 1 birim Y vardır.
- %75 X olduğuna göre, %25 Y vardır.
2x / (2x + y) = 0.75
Bu eşitlikten y’yi x cinsinden bulabiliriz:
\Rightarrow \frac{2x}{2x + y} = 0.75
2x = 0.75 (2x + y)
2x = 1.5x + 0.75y
0.5x = 0.75y
y = \frac{0.5}{0.75}x
y = \frac{2}{3}x
2. İkinci Bileşiğin Analizi:
İkinci bileşik %60 X ve %40 Y içeriyor.
Varsayalım ki ikinci bileşik X_mY_n formülüne sahiptir.
m = 1 ve n = 1 için, X ve Y oranlarını kontrol edelim:
\frac{mx}{mx + ny} = 0.60
mx = 0.60(mx + ny)
mx = 0.60mx + 0.60ny
0.40mx = 0.60ny
\frac{m}{n} = \frac{0.60y}{0.40x}
Daha önce bulduğumuz y = \frac{2}{3}x ifadesini yerine koyarsak:
\frac{m}{n} = \frac{0.60(\frac{2}{3}x)}{0.40x}
\frac{m}{n} = \frac{0.60 \cdot \frac{2}{3}}{0.40}
\frac{m}{n} = \frac{0.4}{0.4} \cdot \frac{2}{3}
\frac{m}{n} = 1 \cdot \frac{2}{3}
Bu oran X_3Y_2 formülüne karşılık gelir.
Sonuç olarak, doğru seçenek D) X_3Y_2'dir.